Основные свойства орицикла

1.Каждый орицикл полностью определяется заданием одной его осью и одной его точкой.

2.Какая-либо прямая с орициклом может иметь не больше двух общих точек.

3.Точка пересечения прямой 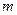, проведенной через середину хорды 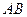орицикла перпендикулярно к этой хорде, с орициклом есть вершина орицикла.

4.Все внутренние точки хорды орицикла лежат в середине орицикла, а все внешние точки хорды лежат вне орицикла.

5.Орицикл – выгнутая кривая линия, выпуклостью направленную в сторону, противоположную направлению параллельности.

6.Орицикл не зависит от того, какую из точек взять за первую.

7.Один и тот же пучок параллельных прямых определяет бесконечно много орициклов, причем равных между собой.

8.Каковы бы ни были две точки А и В плоскости, через них можно провести точно два орицикла, симметричных относительно прямой АВ.

9.Все точки орицикла лежат по одну сторону от перпендикуляра, проведенного в какой-либо вершине к оси, а точнее в сторону параллельности осей. Итак, каждая ось орицикла есть нормалью.

10.Орицикл можно рассматривать как предельное положение окружности с бесконечно удаленным центром.