Функция Лобачевского

Рассмотрим свойства углов параллельности. Первое, изменяя угол параллельности, меняется длина перпендикуляра (рис.27).

Пусть (рис.28).

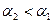Поскольку , то . С другой стороны, . Отсюда выходит, что . Таким образом, с возрастанием угол параллельности уменьшается.

Можно показать, что значение угла параллельности при данном значении не зависит от выбора прямой и точки на ней, то есть для данного значении угол параллельности имеет определенное одно и тоже значение, какую бы ни взяли прямую и где бы ни взяли на ней точку.

Действительно, пусть 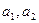- две произвольные прямые, - произвольные точки этих прямых (рис. 29).

Восстановим в этих точках перпендикулярах к данным прямым и отложим на них отрезки Через точки проведем прямые Пусть - соответственно углы параллельности. Допустим, что 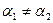, например, . Тогда, откладывая угол 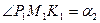, получим луч 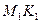, проходящий в середине угла и пересекает в точке .

Отложим на прямой . Тогда 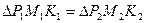по двум катетам, отсюда выходит, что луч совпадает с , что не возможно, поскольку пересекает , а не пересекает. И так, неравенство невозможно. Аналогично, доказывается невозможность неравенства . Итак, , что и требовалось доказать.

Таким образом, мы приходим к выводу, что каждому значению соответствует вполне определенное значение угла параллельности , такое, что есть функция с областью определения . Эта функция обозначается и называется функцией Лобачевского.

Н.И. Лобачевский нашел аналитическую формулу для функции :

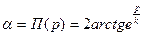, где 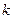- некоторая положительная постоянная. Анализируя эту формулу, получаем

Это означает, что при достаточно малом угол параллельности . Поэтому при достаточно малых пространство Лобачевского как угодно мало отличается от пространства Евклида, и, евклидову геометрию можно рассматривать как предельный случай геометрии Лобачевского, если , то есть при малых размерах.

Есть еще один случай, когда пространство Лобачевского переходит евклидово. Рассмотрим постоянную 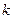в формуле Лобачевского. Эта постоянная может принимать значения от 0 до 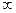, и для каждого будет существовать свое пространство Лобачевского. Эти пространства будут отличаться одно от другого степенью отклонения от евклидового пространства. Действительно,

Поэтому чем больше 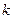, тем меньше пространство Лобачевского будет отличаться от евклидового. Выясняется, что постоянная 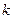- это радиус кривизны пространства Лобачевского. Итак, пространство Лобачевского будет тем ближе к евклидову, чем большего радиус кривизны, то есть чем меньше его кривизна.