Теоремы про серединные перпендикуляры к сторонам треугольника и следствия из них

Теорема 6. Если два серединных перпендикуляра к сторонам треугольника пересекаются, то и третий серединный перпендикуляр проходит через эту точку пересечения.

Доказательство.

В геометрии Евклида каждая точка серединного перпендикуляра отрезка равноудалена от его концов. Это утверждение доказывается на основе равенства треугольников, поэтому справедливо и на плоскости Лобачевского. Если точка где то Отсюда тогда точка О лежит и на третьем серединном перпендикуляре треугольника (рис.36).

Следствие. Если два серединных перпендикуляра к сторонам треугольника пересекаются в точке О, то около такого треугольника можно описать окружность с центром в точке О.

Теорема 7. Если два серединных перпендикуляра к сторонам треугольника расходятся, то и серединный перпендикуляр к третьей стороне расходится с двумя первыми и все имеют единственный общий перпендикуляр, причем все вершины треугольника равноудалены от него.

Доказательство. Пусть в треугольнике точки 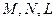- середины сторон соответственно. и прямые - расходятся (рис. 37).

Тогда прямые имеют единственный общий перпендикуляр а, такой что Опустим из вершин треугольника перпендикуляры на прямую а: Раньше было доказано, что в четырехугольнике Саккери перпендикуляр, проведенный через середину одного основания, перпендикулярен и к другому основанию. Справедливо и обратное утверждение: если в четырехугольнике перпендикуляр, проведенный через середину одной стороны, перпендикулярный и к противоположной стороне, то такой четырехугольник есть четырехугольником Саккери. На основе этой теоремы четырехугольники - четырехугольники Саккери, поэтому Тогда - тоже четырехугольник Саккери, в нем серединный перпендикуляр основания будет серединным перпендикуляром и основания . А это означает, что расходится с .

Следствие. Если серединные перпендикуляры к двум сторонам треугольника расходятся, то около треугольника можно описать эквидистанту.

Теорема 8. Если два серединных ориентированных в одну сторону к сторонам треугольника перпендикуляра параллельны, то и серединный перпендикуляр к третьей стороне треугольника параллелен двум первым.

Доказательство. Справедливость этой теоремы выплывает из двух предыдущих. Действительно, если допустить, что серединный перпендикуляр с к стороне АС пересекается с серединным перпендикуляром а к стороне АВ, то по теореме 6 через точку их пересечения должна пройти и третий перпендикуляр в и по теореме 7 должен расходится, что противоречит условию теоремы. Итак, осталось, что серединный перпендикуляр с должен быть параллелен а и в.

Следствие. Если серединные перпендикуляры к двум сторонам треугольника параллельны в данном направлении, то около такого треугольника можно описать орицикл.

Из данных теорем вытекает, что на плоскости Лобачевского около каждого треугольника можно описать одну из трех линий – или окружность, или эквидистанту, или орицикл.