|
| | Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, кроме того, что:
|
| | 515.1
| ее оси 2a=10 и 2b=8;

|
| | 515.2
| расстояние между фокусами 2c=10 и ось 2b=8;

|
| | 515.3
| расстояние между фокусами 2c=6 и эксцентриситет e=3/2;
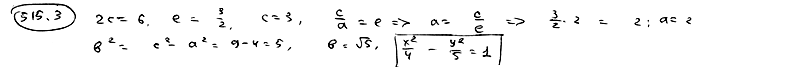
|
| | 515.4
| ось 2a=16 и эксцентриситет e=5/4;

|
| | 515.5
| уравнения асимптот  и расстояние между фокусами 2c=20; и расстояние между фокусами 2c=20;

|
| | 515.6
| расстояние между директрисами равно 228/13 и расстояние между фокусами 2c=26;

|
| | 515.7
| расстояние между директрисами равно 32/5 и ось 2b=6;

|
| | 515.8
| расстояние между директрисами равно 8/3 и эксцентриситет e=3/2;

|
| | 515.9
| уравнения асимптот  и расстояние между директрисами равно 64/5; и расстояние между директрисами равно 64/5;

|
|
| | Составить уравнение гиперболы, фокусы которого расположены на оси ординат симметрично относительно начала координат, зная, кроме того, что:
|
| | 516.1
| ее полуоси a=6, b=18 (буквой а мы обозначаем полуось гиперболы, расположенной на оси абсцисс);

|
| | 516.2
| расстояние между фокусами 2с=10 и эксцентриситет e=5/3;

|
| | 516.3
| уравнения асимптот  и расстояние между вершинами равно 48; и расстояние между вершинами равно 48;

|
| | 516.4
| расстояние между директрисами равно 50/7 и эксценриситет e=7/5;

|
| | 516.5
| уравнения асимптот  и расстояние между директрисами равно 32/5. и расстояние между директрисами равно 32/5.

|
|
| | Определить полуоси а и b каждой из следующих гипербол:
|
| | 517.1
|  ; ;
|
| | 517.2
|  ; ;
|
| | 517.3
|  ; ;
|
| | 517.4
|  ; ;
|
| | 517.5
|  ; ;
|
| | 517.6
|  ; ;
|
| | 517.7
|  . .

|
|
| | Дана гипербола  . Найти: полуоси а и b, фокусы, эксцентриситет, уравнения асимптот, уравнения директрис. . Найти: полуоси а и b, фокусы, эксцентриситет, уравнения асимптот, уравнения директрис.

|
|
| | Дана гипербола  . Найти: полуоси а и b, фокусы, эксцентриситет, уравнения асимптот, уравнения директрис. . Найти: полуоси а и b, фокусы, эксцентриситет, уравнения асимптот, уравнения директрис.

|
|
| | Вычислить площадь треугольника, образованного асимптотами гиперболы  и прямой и прямой  . .
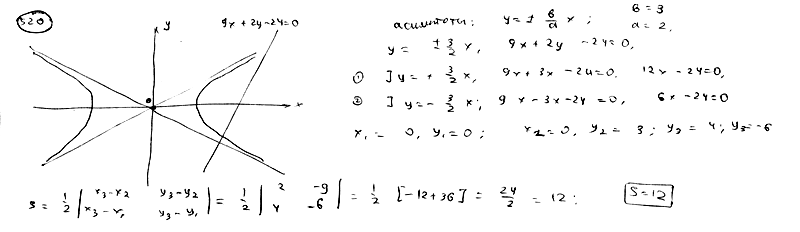
|
|
| | Установить, какие линии определяются следующими уравнениями. Изобразить эти линии на чертеже.
|
| | 521.1
|  ; ;
|
| | 521.2
|  ; ;
|
| | 521.3
|  ; ;
|
| | 521.4
|  . .

|
|
| | Дана точка M1(10;  ) на гиперболе ) на гиперболе  . Составить уравнения прямых, на которых лежат фокальные радиусы точки М1. . Составить уравнения прямых, на которых лежат фокальные радиусы точки М1.

|
|
| | Убедившись, что точка М1(-5; 9/4) лежит на гиперболе  , определить фокальные радиусы точки М1. , определить фокальные радиусы точки М1.

|
|
| | Эксцентриситет гиперболы e=2, фокальный радиус ее точки М, проведенный из некоторого фокуса, равен 16.
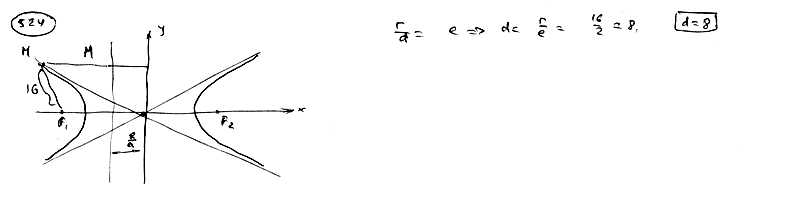 Вычислить расстояние от точки М до односторонней с этим фокусом директрисы. Вычислить расстояние от точки М до односторонней с этим фокусом директрисы.
|
|
| | Эксцентриситет гиперболы e=3, расстояние от точки М гиперболы до директрисы e=3, расстояние от точки М гиперболы до директрисы равно 4. Вычислить расстояние от точки М до фокуса, одностороннего с этой директрисой.
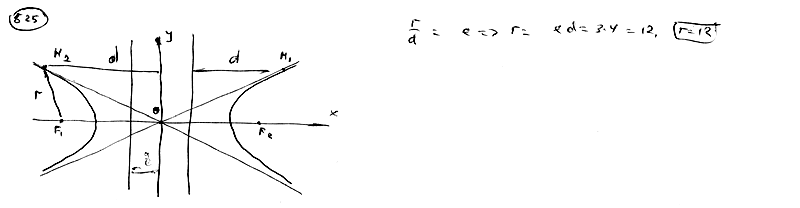
|
|
| | Эксцентриситет гиперболы e=2, центр ее лежит в начале координат, один из фокусов F(12; 0). Вычислить расстояние от точки М1 гиперболы с абсциссой, равной 13, до директрисы, соответствующей заданному фокусу.

|
|
| | Эксцентриситет гиперболы e=3/2, центр ее лежит в начале координат, одна из директрис дана уравнением x=-8. Вычислить расстояние от точки М1 гиперболы с абсциссой, равной 10, до фокуса, соответствующего заданной директрисе.

|
|
| | Определить точки гиперболы  , расстояние от которых до правого фокуса равно 4,5. , расстояние от которых до правого фокуса равно 4,5.

|
|
| | Определить точки гиперболы  , расстояние которых до левого фокуса равно 7. , расстояние которых до левого фокуса равно 7.

|
|
| | Через левый фокус гиперболы  проведен перпендикуляр к ее оси, содержащей вершины. Определить расстояние от фокусов до точек пересечения этого перпендикуляра с гиперболой. проведен перпендикуляр к ее оси, содержащей вершины. Определить расстояние от фокусов до точек пересечения этого перпендикуляра с гиперболой.

|
|
| | Пользуясь одним циркулем, построить фокусы гиперболы  (считая, что оси координат изображены и масштабная единица задана). (считая, что оси координат изображены и масштабная единица задана).

|
|
| | Составить уравнение гиперболы, фокусы которой лежат на оси абсцисс симметрично относительно начала координат, если даны:
|
| | 532.1
| точки M1(6; -1), M2(-8;  ) гиперболы; ) гиперболы;

|
| | 532.2
| точка М1(-5; 3) гиперболы и эксцентриситет e=  ; ;

|
| |
532.3
| точка М1(9/2; -1) гиперболы с уравнения асимптот  ; ;

|
| |
532.4
| точка М1(-3; 5/2) гиперболы и уравнения директрис  ; ;

|
| | 532.5
| уравнения асимптот  и уравнения директрис и уравнения директрис  . .

|
|
| | Определить эксцентриситет равносторонней гиперболы.

|
|
| | Определить эксцентриситет гиперболы, если отрезок между ее вершинами виден из фокусов сопряженной гиперболы под углом 600.

|
|
| | Фокусы гиперболы совпадают с фокусами эллипса  . Составить уравнение гиперболы, если ее эксцентриситет e=2. . Составить уравнение гиперболы, если ее эксцентриситет e=2.

|
|
| | Составить уравнение гиперболы, фокусы которой лежат в вершинах эллипса  , а директрисы проходят через фокусы этого эллипса. , а директрисы проходят через фокусы этого эллипса.

|
|
| | Доказать, что расстояние от фокуса гиперболы  до ее асимптоты равно b. до ее асимптоты равно b.

|
|
| | Доказать, что произведение расстояний от любой точки гиперболы  до двух ее асимптот есть величина постоянная, равная до двух ее асимптот есть величина постоянная, равная  . .

|
|
| | Доказать, что площадь параллелограмма, ограниченного асимптотами гиперболы  и прямыми, проведенными через любую ее точку параллельно асимптотами, есть величина постоянная, равная ab/2. и прямыми, проведенными через любую ее точку параллельно асимптотами, есть величина постоянная, равная ab/2.

|
|
| | Составить уравнение гиперболы, если известны ее полуоси a и b, центр C(x0; y0) и фокусы расположены на прямой:
|
| | 540.1
| параллельной оси Ox;
|
| | 540.2
| параллельной оси Oy.

|
|
| | Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты ее центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис:
|
| | 541.1
|  ; ;

|
| | 541.2
|  ; ;

|
| | 541.3
|  . .

|
|
| | Установить, какие линии определяются следующими уравнениями. Изобразить эти линии на чертеже.
|
| | 542.1
|  ; ;

|
| | 542.2
|  ; ;

|
| | 542.3
|  ; ;

|
| | 542.4
|  . .

|
|
| | Составить уравнение гиперболы, зная, что:
|
| | 543.1
| расстояние между ее вершинами равно 24 и фокусы суть F1(-10; 2), F2(16; 2);

|
| | 543.2
| фокусы суть F1(3; 4), F2(-3; -4) и расстояние между директрисами равно 3,6;

|
| | 543.3
| угол между асимптотами равен 900 и фокусы суть F1(4; -4), F2(-2; 2).

|
|
| | Составить уравнение гиперболы, если известны ее эксцентриситет e=5/4, фокус F(5; 0) и уравнение соответствующей директрисы  . .

|
|
| | Составить уравнение гиперболы, если известны ее эксцентриситет e=13/12, фокус F(0; 13) и уравнение соответствующей директирсы  . .

|
|
| | Точка А(-3; -5) лежит на гиперболе, фокус которой F(-2; -3), а соответствующая директриса дана уравнением  . Составить уравнение этой гиперболы. . Составить уравнение этой гиперболы.

|
|
| | Составить уравнение гиперболы, если известны ее эксцентриситет e= 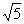 , фокус F(2; -3) и уравнение соответствующей директрисы , фокус F(2; -3) и уравнение соответствующей директрисы  . .

|
|
| | Точка М1(1; -2) лежит на гиперболе, фокус которой F(-2; 2), а соответстующая директриса дана уравнением  . Составить уравнение этой гиперболы. . Составить уравнение этой гиперболы.

|
|
| | Дано уравнение равносторонней гиперболы  . Найти ее уравнение в новой системе, приняв за оси координат ее асимптоты. . Найти ее уравнение в новой системе, приняв за оси координат ее асимптоты.

|
|
| | Установив, что каждое из следующих уравнений определяет гиперболу, найти для каждой из них центр, полуоси, уравнения асимптот и построить их на чертеже:
|
| | 550.1
|  ; ;
|
| | 550.2
| 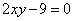 ; ;
|
| | 550.3
| 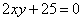 . .

|
|
| | Найти точку пересечения прямой  и гиперболы и гиперболы  . .

|
|
| | Найти точки пересечения прямой  и гиперболы и гиперболы  . .

|
|
| | Найти точки пересечения прямой  и гиперболы и гиперболы  . .

|
|
| | В следующих случаях определить, как расположена прямая относительно гиперболы: пересекает ли, касается или проходит вне ее:
|
| | 554.1
|  , ,  ; ;
|
| | 554.2
|  , ,  ; ;
|
| | 554.3
| 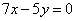 , ,  . .

|
|
| | Определить, при каких значениях m прямая  : :
|
| | 555.1
| пересекает гиперболу  : :
|
| | 555.2
| касается ее;
|
| | 555.3
| проходит вне этой гиперболы.

|
|
| | Вывести условие, при котором прямая  касается гиперболы касается гиперболы  . .

|
|
| | Составить уравнение касательной к гиперболе  в ее точке M1(x1; y1). в ее точке M1(x1; y1).

|
|
| | Доказать, что касательные к гипербле, проведенные в концах одного и того же диаметра, параллельны.

|
|
| | Составить уравнения касательных к гиперболе  , перпендикулярных к прямой , перпендикулярных к прямой  . .

|
|
| | Составить уравнения касательных к гиперболе  , параллельных прямой , параллельных прямой  . .

|
|
| | Провести касательные к гиперболе 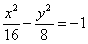 параллельно прямой параллельно прямой  и вычислить расстояние d между ними. и вычислить расстояние d между ними.

|
|
| | На гиперболе  найти точку М1, ближайшую к прямой найти точку М1, ближайшую к прямой  , и вычислить расстояние d от точки М1 до этой прямой. , и вычислить расстояние d от точки М1 до этой прямой.

|
|
| | Составить уравнение касательной к гиперболе  , проведенных из точки А(-1; -7). , проведенных из точки А(-1; -7).

|
|
| | Из точки С(1; -10) проведены касательные к гиперболе  . Составить уравнение хорды, соединяющей точки касания. . Составить уравнение хорды, соединяющей точки касания.

|
|
| | Из точки Р(1; -5) проведены касательные к гиперболе  . Вычислить расстояние d от точки Р до хорды гиперболы, соединяющей точки касания. . Вычислить расстояние d от точки Р до хорды гиперболы, соединяющей точки касания.

|
|
| | Гипербола проходит через точку А( ; 3) и касается прямой ; 3) и касается прямой  . Составить уравнение этой гиперболы при условии, что ее оси совпадают с осями координат. . Составить уравнение этой гиперболы при условии, что ее оси совпадают с осями координат.

|
|
| | Составить уравнение гиперболы, касающейся прямых  , ,  , при условии, что ее оси совпадают с осями координат. , при условии, что ее оси совпадают с осями координат.

|
|
| | Убедившись, что точки пересечения эллипса  и гиперболы и гиперболы  являются вершинами прямоугольника, составить уравнения его сторон. являются вершинами прямоугольника, составить уравнения его сторон.

|
|
| | Даны гиперболы 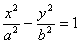 и какая-нибудь ее касательная, Р – точка пересечения касательной с осью Ох, Q – проекция точки касания на ту же ось. Доказать, что и какая-нибудь ее касательная, Р – точка пересечения касательной с осью Ох, Q – проекция точки касания на ту же ось. Доказать, что  . .

|
|
| | Доказать, что фокусы гиперболы расположены по разные стороны от любой ее касательной.

|
|
| | Доказать, что произведение расстояний от фокусов до любой касательной к гиперболе 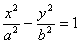 есть величина постоянная, равная b2. есть величина постоянная, равная b2.

|
|
| | Прямая  касается гиперболы, фокусы которой находятся в точках F1(-3; 0), F2(3; 0). Составить уравнение этой гиперболы. касается гиперболы, фокусы которой находятся в точках F1(-3; 0), F2(3; 0). Составить уравнение этой гиперболы.

|
|
| | Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, если известны уравнение касательной к гиперболе  и расстояние между ее вершинами 2а=8. и расстояние между ее вершинами 2а=8.

|
|
| | Доказать, что прямая, касающаяся гиперболы в некоторой точке М, составляет равные углы с фокальными радиусами F1M, F2M и проходит внутри угла F1MF2.

|
|
| | Из правого фокусы гиперболы  под углом под углом 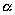 ( (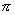 < < 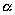 < <  ) к оси Ох направлен луч света. Известно, что ) к оси Ох направлен луч света. Известно, что  . Дойдя до гиперболы, луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч. . Дойдя до гиперболы, луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч.

|
|
| | Доказать, что эллипс и гипербола, имеющие общие фокусы, пересекаются под прямым углом.

|
|
| | Коэффициент равномерного сжатия плоскости к оси Ох равен 4/3. Определить уравнение линии, в котороую при этом сжатии преобразуется гипербола  . .

|
|
| | Коэффициент равномерного сжатия плоскости к оси Оу равен 4/5. Определить уравнение линии, в которую при этом сжатии преобразуется гипербола  . .

|
|
| | Найти уравнение линии, в которую преобразуется гипербола  при двух последовательных равноменых сжатиях плоскости к координатным осям, если коэффициенты равномерного сжатия плоскости к осям Ох и Оу соответствуют 2/3 и 5/3. при двух последовательных равноменых сжатиях плоскости к координатным осям, если коэффициенты равномерного сжатия плоскости к осям Ох и Оу соответствуют 2/3 и 5/3.

|
|
| | Определить коэффициент q равномерного сжатия плоскости к оси Ох, при котором гипербола  преобразуется в гиперболу преобразуется в гиперболу  . .

|
|
| | Определить коэффициент q равномерного сжатия плоскости к оси Оу, при котором гипербола  преобразуется в гиперболу преобразуется в гиперболу  . .

|
|
| | Определить коэффициенты q1, q2 двух последовательных равномерных сжатий плоскости к осям Ох и Оу, при которых гипербола  преобразуется в гиперболу преобразуется в гиперболу  . .

|



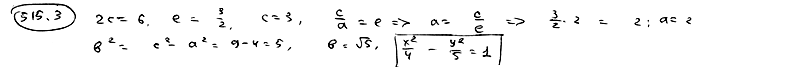

 и расстояние между фокусами 2c=20;
и расстояние между фокусами 2c=20;




 и расстояние между директрисами равно 64/5;
и расстояние между директрисами равно 64/5;



 и расстояние между вершинами равно 48;
и расстояние между вершинами равно 48;


 и расстояние между директрисами равно 32/5.
и расстояние между директрисами равно 32/5.

 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.

 . Найти: полуоси а и b, фокусы, эксцентриситет, уравнения асимптот, уравнения директрис.
. Найти: полуоси а и b, фокусы, эксцентриситет, уравнения асимптот, уравнения директрис.

 . Найти: полуоси а и b, фокусы, эксцентриситет, уравнения асимптот, уравнения директрис.
. Найти: полуоси а и b, фокусы, эксцентриситет, уравнения асимптот, уравнения директрис.

 и прямой
и прямой  .
.
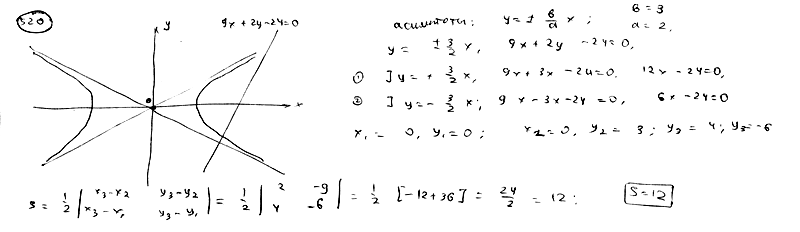
 ;
;
 ;
;
 ;
;
 .
.

 ) на гиперболе
) на гиперболе  . Составить уравнения прямых, на которых лежат фокальные радиусы точки М1.
. Составить уравнения прямых, на которых лежат фокальные радиусы точки М1.

 , определить фокальные радиусы точки М1.
, определить фокальные радиусы точки М1.

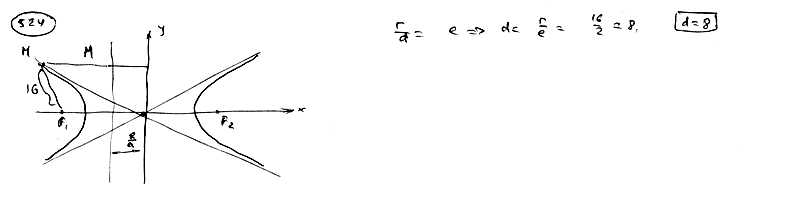 Вычислить расстояние от точки М до односторонней с этим фокусом директрисы.
Вычислить расстояние от точки М до односторонней с этим фокусом директрисы.
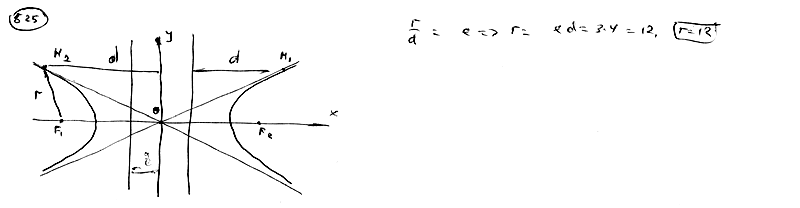


 , расстояние от которых до правого фокуса равно 4,5.
, расстояние от которых до правого фокуса равно 4,5.

 , расстояние которых до левого фокуса равно 7.
, расстояние которых до левого фокуса равно 7.

 проведен перпендикуляр к ее оси, содержащей вершины. Определить расстояние от фокусов до точек пересечения этого перпендикуляра с гиперболой.
проведен перпендикуляр к ее оси, содержащей вершины. Определить расстояние от фокусов до точек пересечения этого перпендикуляра с гиперболой.

 (считая, что оси координат изображены и масштабная единица задана).
(считая, что оси координат изображены и масштабная единица задана).

 ) гиперболы;
) гиперболы;

 ;
;

 ;
;

 ;
;

 и уравнения директрис
и уравнения директрис  .
.



 . Составить уравнение гиперболы, если ее эксцентриситет e=2.
. Составить уравнение гиперболы, если ее эксцентриситет e=2.

 , а директрисы проходят через фокусы этого эллипса.
, а директрисы проходят через фокусы этого эллипса.

 до ее асимптоты равно b.
до ее асимптоты равно b.

 до двух ее асимптот есть величина постоянная, равная
до двух ее асимптот есть величина постоянная, равная  .
.

 и прямыми, проведенными через любую ее точку параллельно асимптотами, есть величина постоянная, равная ab/2.
и прямыми, проведенными через любую ее точку параллельно асимптотами, есть величина постоянная, равная ab/2.


 ;
;

 ;
;

 .
.

 ;
;

 ;
;

 ;
;

 .
.




 .
.

 .
.

 . Составить уравнение этой гиперболы.
. Составить уравнение этой гиперболы.

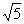 , фокус F(2; -3) и уравнение соответствующей директрисы
, фокус F(2; -3) и уравнение соответствующей директрисы  .
.

 . Составить уравнение этой гиперболы.
. Составить уравнение этой гиперболы.

 . Найти ее уравнение в новой системе, приняв за оси координат ее асимптоты.
. Найти ее уравнение в новой системе, приняв за оси координат ее асимптоты.

 ;
;
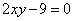 ;
;
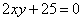 .
.

 и гиперболы
и гиперболы  .
.

 и гиперболы
и гиперболы  .
.

 и гиперболы
и гиперболы  .
.

 ,
,  ;
;
 ,
,  ;
;
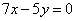 ,
,  .
.

 :
:
 :
:

 касается гиперболы
касается гиперболы  .
.

 в ее точке M1(x1; y1).
в ее точке M1(x1; y1).


 , перпендикулярных к прямой
, перпендикулярных к прямой  .
.

 , параллельных прямой
, параллельных прямой  .
.

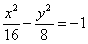 параллельно прямой
параллельно прямой  и вычислить расстояние d между ними.
и вычислить расстояние d между ними.

 найти точку М1, ближайшую к прямой
найти точку М1, ближайшую к прямой  , и вычислить расстояние d от точки М1 до этой прямой.
, и вычислить расстояние d от точки М1 до этой прямой.

 , проведенных из точки А(-1; -7).
, проведенных из точки А(-1; -7).

 . Составить уравнение хорды, соединяющей точки касания.
. Составить уравнение хорды, соединяющей точки касания.

 . Вычислить расстояние d от точки Р до хорды гиперболы, соединяющей точки касания.
. Вычислить расстояние d от точки Р до хорды гиперболы, соединяющей точки касания.

 ; 3) и касается прямой
; 3) и касается прямой  . Составить уравнение этой гиперболы при условии, что ее оси совпадают с осями координат.
. Составить уравнение этой гиперболы при условии, что ее оси совпадают с осями координат.

 ,
,  , при условии, что ее оси совпадают с осями координат.
, при условии, что ее оси совпадают с осями координат.

 и гиперболы
и гиперболы  являются вершинами прямоугольника, составить уравнения его сторон.
являются вершинами прямоугольника, составить уравнения его сторон.

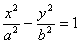 и какая-нибудь ее касательная, Р – точка пересечения касательной с осью Ох, Q – проекция точки касания на ту же ось. Доказать, что
и какая-нибудь ее касательная, Р – точка пересечения касательной с осью Ох, Q – проекция точки касания на ту же ось. Доказать, что  .
.


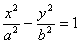 есть величина постоянная, равная b2.
есть величина постоянная, равная b2.

 касается гиперболы, фокусы которой находятся в точках F1(-3; 0), F2(3; 0). Составить уравнение этой гиперболы.
касается гиперболы, фокусы которой находятся в точках F1(-3; 0), F2(3; 0). Составить уравнение этой гиперболы.

 и расстояние между ее вершинами 2а=8.
и расстояние между ее вершинами 2а=8.


 под углом
под углом 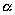 (
(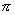 <
< 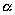 <
<  ) к оси Ох направлен луч света. Известно, что
) к оси Ох направлен луч света. Известно, что  . Дойдя до гиперболы, луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч.
. Дойдя до гиперболы, луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч.


 .
.

 .
.

 при двух последовательных равноменых сжатиях плоскости к координатным осям, если коэффициенты равномерного сжатия плоскости к осям Ох и Оу соответствуют 2/3 и 5/3.
при двух последовательных равноменых сжатиях плоскости к координатным осям, если коэффициенты равномерного сжатия плоскости к осям Ох и Оу соответствуют 2/3 и 5/3.

 преобразуется в гиперболу
преобразуется в гиперболу  .
.

 преобразуется в гиперболу
преобразуется в гиперболу  .
.

 преобразуется в гиперболу
преобразуется в гиперболу  .
.

