 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Роль симметрии в евклидовой геометрии
|
|
Понятие симметрии вводится через понятие движения, т.к. люб движение евклид геометрии и неевклид геометрии Лобачевкого есть композиция осевых симметрий.Движения:1паралл. Перенос на в-р  :τ
:τ  2.осевая симм отн ι:Sι 3.поворот на угол φ:
2.осевая симм отн ι:Sι 3.поворот на угол φ: 
 4. Скользящая симметрия Каждое из этих движений представимо в произ симметрий
4. Скользящая симметрия Каждое из этих движений представимо в произ симметрий


 P- сер [M,
P- сер [M,  ] Q- сер [
] Q- сер [  ,
,  ]
] 
 перп ι,
перп ι, 
M 


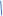

 перп m, | M
перп m, | M  |=|
|=|  |,
|, 
 ,
, 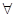 м=>
м=> 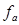 (М)=
(М)=  M
M 

τ 
 =
=  .
.  ||ι, M
||ι, M  -симм ι M
-симм ι M  =
=  f-скольз. симметрия P
f-скольз. симметрия P  Q
Q
Понятия «точки» и «прямые» могут быть определены через движения. Ι m
A<=> 
ι<=> 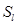 -ед. осевая симметрия
-ед. осевая симметрия
Евклидова и неевклид. Геометрии могут исслед из аксиом или на 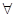 модели.При построении модели геом Лобачевского будет использ движение для описания неевклид движений.
модели.При построении модели геом Лобачевского будет использ движение для описания неевклид движений.
Все теоремы евлид и неевкл геометрий можно вывести с помощью движений. Напр. Точки и прямые определяются через движения.
15.
В классических метрических геометриях (евклидовых), не евклидовой геометрии Лобочевского, сферической или элептической геометрии Римена ключевую роль играет движение без опоры на теорию параллельности сущ аксиоматики в которых движение входит в число первоночальных понятий. Соответствия аксиомы двух движений в таких аксиоматиках довольно сложные наиболее удобно вводить движения через понятия осевой симетри. Это возможно потому что любое движение в евклидовой геометрии и не евклидовой геометрии Лобочевского.
Для любого движения в евклидовой плоскости:
1. Параллельный перенос на вектор а.
2. Осевая симметрия
3. Скользящая симметрия
4. R-ротер.
Покажем, что каждая из этих движений раскладывается вкомпозицию или симметрию
Sl- осевая симметрия
RH0-поворот вокруг т M0 на угол фи.
Ta- параллельный перенос на вектор а
m∩l=M0
ϕ>0 против час стрелке, ϕ<0 по часовой стрелке |M0M’|=|M0M”|=|M0M|
a+b=4/2
угол M’OM”=2a+2b=ϕ
|M0M|=|M0M’| => Rϕ M0(M)=M” Для любых M => Rϕ M0=SmSl
Вектор MM’ перпендикулярен l M’M” перпендикулярно m
P середина [MM”], Q- сер [M’M”], [MM”] =|вектору а|, вектор MM”=вектору а
Та=SmSl Ta(M)=M”
Ta=SMSW f=Ual=SmSnSl
F=TaSl
Дата публикования: 2015-10-09; Прочитано: 393 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
