Перемещения при изгибе. Расчеты на жесткость

При деформации балки центры тяжести ее поперечных сечений получают линейные перемещения, а сами сечения поворачиваются вокруг своих нейтральных осей.

Допущение о малости перемещений позволяет считать, что направление линейных перемещений перпендикулярно продольной оси недеформированной балки. Эти перемещения называют прогибами. Ось изогнутой балки условно называют изогнутой осью или упругой линией. Так как при изгибе справедлива гипотеза Я. Бернулли, то угол θ поворота поперечного сечения равен углу между касательной к упругой линии в данной точке и осью недеформированной балки (рисунок 198).

Условие жесткости выражается неравенством , (104)

где δ – максимальный прогиб, называемый стрелой прогиба, а [δ] - допускаемый прогиб.

Рисунок 198

Обычно 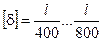, где l – пролет балки.

Для обеспечения нормальной работы подшипников иногда ставится дополнительное условие жесткости – ограничение угла поворота опорных сечений

θ_{оп max} ≤ [θ] (105)

[θ] ≈ 0,001 рад.

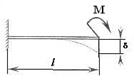
Максимальный прогиб δ обычно определяют с помощью таблиц и использования принципа независимости действия сил (таблица 21).

Таблица 21

Схема нагружения балки	Максимальный прогиб