Продолжение таблицы 9

Выполняемое действие	Иллюстрация действия
	Отбрасываем связь (заделку) и заменяем ее реакциями RАХ, RAY, MR, которые должны уравновесить внешние силы. Если направления реакций не известны или непонятны, то направляем их со знаком плюс: RAY – вверх, по оси Y; RАХ – вправо, по оси Х; MR – по часовой стрелке.
	Проводим оси координат – так, чтобы одна из осей проходила по неизвестной реакции. Начало координат принимаем в точке А (можно в любой точке А, В или С).
	За центр моментов принимаем точку опоры А.
	Составляем уравнения равновесия (например, по 1 форме)
	Решаем уравнения равновесия и определяем неизвестные силы. (Реакции вычислять до сотых).	RАХ = 0; RAY = -F = -10 кН; Знак минус показывает, что сила реакции RAY направлена в противоположную сторону. МR = F·AC – М = F·5 – М = 10·5 – 6 = = 44 кН·м Направление момента МR выбрано верно.
	Проверка правильности решения. Должны получить тождество 0 = 0 или 0 ≈ 0 (например, 0,02 0). Для проверки нельзя использовать уравнение моментов относительно точки опоры, так как мы не сможем проверить реакцию RAY.	МR + RAY·2 + М – F·3 = 0; 44 – 10·2 + 6 – 10·3 = 0; 0 = 0 Реакции определены верно. ИЛИ МR + RAY·5 + М = 0; 44 – 10·5 + 6 = 0; 0 = 0 Реакции определены верно.
	Ответ RАХ = 0; RAY = -10 кН; МR = 44 кН·м.

1 Пара сил проекций на оси не дает и в уравнения 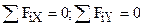момент М не входит.

2 Пара сил входит в уравнение моментов относительно любой точки со своим М с учетом его направления вращения.

3 Равномерно распределенную нагрузку заменяем ее равнодействующей F_q = q· l, приложенной посередине участка l.

4 Силу F, наклоненную к оси Х, можно разложить на вертикальную F_Y и горизонтальную F_Х составляющие.

Подумай и ответь на вопросы

30 Найти ? (рисунок 55).

1) ; 2) ; 3) .

31 Какому виду опор (рисунок 56) соответствует указанная реакция связи?

Рисунок 55 Рисунок 56

32 Какому виду опор (рисунок 57) соответствуют указанные реакции связи?

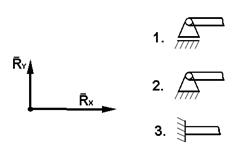
Рисунок 57 Рисунок 58

Пример 10. Определить реакции опор шарнирно закрепленной балки

(рисунок 58-а)

Решение

1 Выбираем балку АВ и прикладываем к ней М.

2 Заменим распределенную нагрузку ее равнодействующей F_q, приложенной посередине участка АС

F_q = q· l = 4·2 = 8 кН.

3 Заменим силу F, наклоненную к оси балки, ее составляющими: силами F_Х и F_Y.

Для этого проводим силу F так, как она показана на схеме (рисунок 58-в).

Из начала и конца силы F проводим горизонтальные и вертикальные линии. В полученном прямоугольнике показываем составляющие силы так, чтобы все три силы F, F_Х и F_Y выходили из одной точки.

Переносим силы F_Х и F_Y на расчетную схему (рисунок 58-б) в точку их приложения D.

Вычисляем модули сил

F_Х = F·cos30^о = 10·0,866 = 8,66 кН;

F_Y = F·cos60^о = 10·0,5 = 5 кН.

4 Отбрасываем шарнирно-неподвижную опору А и шарнирно-подвижную опору В и заменяем их реакциями R_АХ, R_AY и R_В.

Причем, реакцию R_АХ сразу можно направить правильно – противоположно силе F_Х, которую реакция уравновешивает.

Реакции R_AY и R_В направим со знаком плюс.

5 Составляем и решаем уравнения равновесия

; ;

; ;

; ;

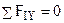R_AX = F_X = 8,66 кН;

;

R_AY = F_q + F_Y –R_B = 8 + 5 – 4 = 9 кН.