Каскад реакторов. Селективность процесса

Единичный реактор идеального смешения не дает высокой степени превращения, так как концентрация исходных реагентов в нем мгновенно падает до конечного значения. Поэтому применяют ряд последовательно расположенных непрерывных реакторов смешения – каскад реакторов – К-РИС (рис. 2.15). Концентрация CА в такой системе падает до конечного значения не сразу, а постепенно, от реактора к реактору (рис. 2.16). В каждом реакторе концентрация компонента в объеме постоянна и равна концентрации на выходе из реактора. Изменение концентрации в реакторах происходит мгновенно скачком при входе реакционной смеси в реактор.

Рабочая концентрация CA в каскаде реакторов в общем выше, чем в единичном реакторе смешения и приближается с увеличением числа реакторов к значению ее в реакторе вытеснения.

Чем больше степеней изменения концентрации в каскаде m (чем больше реакторов), тем больше каскад реакторов приближается к реактору идеального вытеснения (рис.2.16). Выдача расчета каскада реакторов заключается в определении числа ступеней (числа реакторов) – m, необходимых для достижения заданной степени превращения xA.

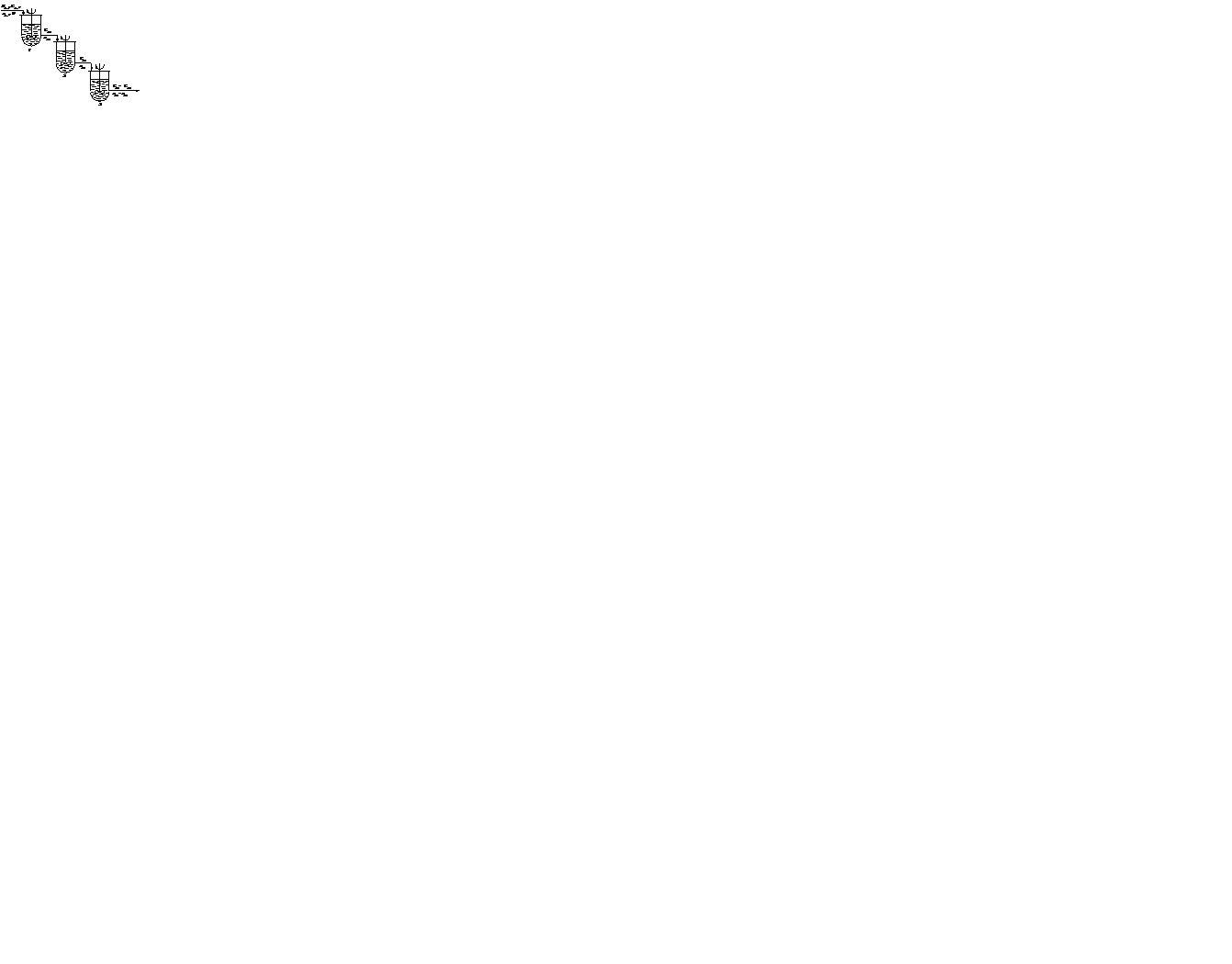
Рис. 2.15 – Каскад реакторов идеального смешения

Существуют аналитический и графический методы расчета каскада реакторов. Аналитический метод выгодно применять при протекании реакции первого порядка, а для реакций более высоких порядков удобнее второй – графический метод.

Рис. 2.16 – Изменение концентрации реагента А в каскаде реакторов идеального смешения

Для расчета каскада реакторов необходимо:

1) иметь сведения о кинетике процесса [- rA = f (CA)],

2) знать концентрацию исходного реагента А на входе в первый реактор, CA o, и на выходе из последнего реактора, CAm, то есть общую степень превращения xA,

3) задаться объемом единичного реактора (то есть временем пребывания в единичном реакторе смешения, см), при этом предполагают, что объемы единичных реакторов в каскаде равны.

Для единичного m -го реактора идеального смешения, исходя из уравнения (2.52), имеем:

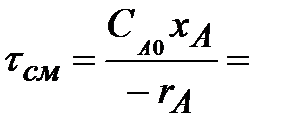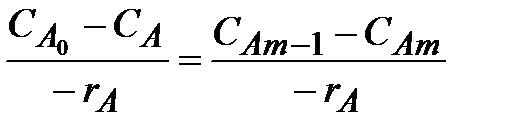
	(2.70)
где CAm- 1, CAm – концентрации компонента A на входе в m-й реактор и на выходе из него.

Из уравнения (2.70) можно найти скорость процесса в реакторе. Для этого представим его в таком виде:

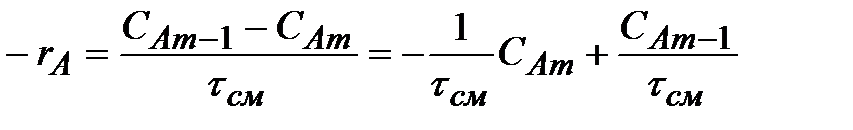
(2.71)

Концентрация реагента на входе в реактор, CAm- 1, и время пребывания, см, – величины известные и постоянные, так как даются по условию. Таким образом, из уравнения (2.71) следует, что скорость реакции (- rA) линейно зависит только от концентрации на выходе, CAm. Если эту зависимость выразить графически, то прямая, описываемая уравнением (2.71), пересекает ось абсцисс в точке СAm- 1 и имеет тангенс угла наклона a, равный 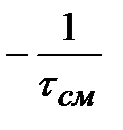(рис.2.17). Для нахождения концентрации в m -ом реакторе необходимо уравнение (2.71) решить совместно с кинетическим уравнением (2.11), то есть:

	(2.72)
Рис. 2.17 – Графический способ расчета каскада реакторов

Поэтому, для нахождения концентрации реагента на выходе из первого реактора, CA 1, необходимо из точки CA o, лежащей на оси абсцисс, провести прямую с тангенсом наклона 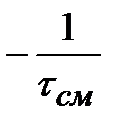до пересечения с кривой - rA = f (CA) в точке М.

Если опустить перпендикуляр из точки пересечения прямой и кривой (точка М, см. рис. 2.17), то на оси абсцисс можно получить значение концентрации CA 1 в первом реакторе. Эта же концентрация является входной для второго реактора. Для нахождения концентрации во втором реакторе CA 2 операция повторяется из точки CA 1. Такие операции продолжают повторять до тех пор, пока в последнем реакторе не будет достигнута заданная конечная концентрация CAк. Так как время пребывания во всех реакторах одинаково, то постоянен угол наклона прямых и, следовательно, они параллельны.

Число ступеней изменения концентрации и будет числом реакторов в каскаде, необходимым для достижения заданной степени превращения xAк.

Как было показано ранее, с увеличением числа реакторов в каскаде характер изменения параметров в нем приближается к реактору идеального вытеснения. Поэтому при увеличении числа реакторов в системе будут сильнее проявляться все свойства, присущие реактору идеального вытеснения, и наоборот.

В качестве примера на рисунке 2.18 приведена зависимость степени превращения от величины k (где k – константа скорости реакции) для реакции первого порядка в каскаде с различным числом реакторов m; произведение k характеризует общий объем системы.

1 – одиночный РИС-Н (m =1); 2 – каскад РИС-Н (m =2); 3 – каскад РИС-Н (m =3); 4 – каскад РИС-Н (m →∞) и РИВ.

Рис. 2.18 – Зависимость хА от k для каскада реакторов с различным m

Из рисунка 2.18 видно, что при одинаковом объеме каскада (k) степень превращения xA повышается с увеличением числа реакторов в каскаде, приближаясь к степени превращения, получаемой в реакторе идеального вытеснения (при m  ¥). Если же сравнить каскады, где получена одна и та же степень превращения xA, то общий объем системы будет меньше там, где взято большее число реакторов [(k)2 < (k)1] (рис.2.18). Меняя число реакторов в каскаде, можно влиять не только на степень превращения xA, но и на селективность процесса и выход целевого продукта (для сложной реакции). При этом необходимо учитывать, что с уменьшением числа реакторов каскад будет давать эффект, близкий к эффекту в реакторе смешения, а с увеличением числа ступеней в системе характер связи между степенью превращения, селективностью и выходом целевого продукта становится таким, как и в реакторе вытеснения.