Классификация реакторов по гидродинамическому режиму. Уравнение материального баланса реакторов

При классификации реакторов принимают во внимание следующие признаки:

- Характер протекающей в реакторе операции.

- Режим движения реакционной среды.

- Тепловой режим.

- Фазовое состояние реагентов.

По первому признаку этой классификации реакторы делятся на периодические, непрерывные и полунепрерывные.

Реакторы с непрерывной подачей реагентов делят, в свою очередь, по характеру движения реакционной среды (по гидродинамической обстановке в реакторе) на реакторы идеального вытеснения, реакторы идеального смешения. Классификация реакторов по тепловому режиму будет дана ниже.

Обычно изучают реакторы в два этапа: вначале при работе их в изотермических условиях, когда температура реакционной смеси постоянна, а затем с учетом изменения температуры реакционной смеси.

Исходным уравнением для получения характеристического уравнения реактора любого типа является материальный баланс, составленный по одному из компонентов реакционной смеси. Составим материальный баланс по исходному веществу А при проведении простой необратимой реакции:

А→R

(1.2)

В общем виде уравнение материального баланса записывается так:

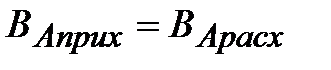,	(1.3)
где ВАприх. – количество вещества А, поступающее в единицу времени в тот реакционный объем, для которого составляется баланс; ВАрасх. – количество вещества А, расходуемое в единицу времени в реакционном объеме.

Учитывая, что поступившее в реактор вещество А расходуется в трех направлениях, можно записать

,	(1.4)
где ВАхр – количество вещества А, вступающее в реакционном объеме в химическую реакцию в единицу времени; ВАст. – сток вещества А (количество вещества А, выходящее из реакционного объема в единицу времени); ВАнак. – накопление вещества А (количество вещества А, остающееся в реакционном объеме в неизменном виде в единицу времени).

С учетом уравнения (1.4) уравнение (1.3) записывается в виде

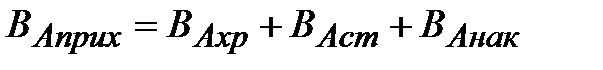
(1.5)

Разность между количеством вещества А, поступающим в единицу времени в реактор (ВАприх.) и выходящим из него (ВАст) – это количество вещества А, переносимое конвективным потоком (ВАконв):_.

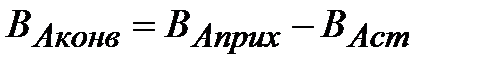
(1.6)

Принимая это во внимание, уравнение (1.5) можно записать еще в одной форме:

(1.7)

В каждом конкретном случае уравнение материального баланса принимает различную форму. Он может составляться для единицы объема реакционной массы либо для реактора в целом. При этом можно рассчитывать материальные потоки, проходящие через объем за единицу времени, а можно относить эти потоки к молю одного из исходных реагентов.

Так, в общем случае, когда состав, температура и другие параметры непостоянны в различных точках реактора или непостоянны во времени, материальный баланс составляют в дифференциальной форме для элементарного объема реактора. В результате получают уравнение конвективного массообмена (А.Г.Касаткин. Основные процессы и аппараты химической технологии, – М: Химия, 1973.), дополненное членом rA, учитывающим протекание химической реакции. Составленное по исходному реагенту А, оно имеет вид:

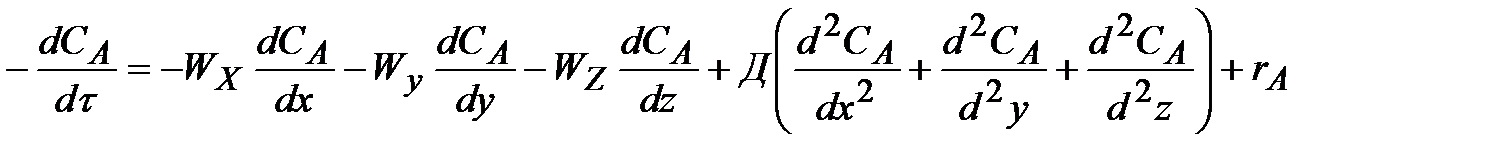,	(1.8)
где CA – концентрация вещества А в реакционной смеси; х, y, z – пространственные координаты; Д – коэффициент молекулярной и турбулентной диффузии; rA – скорость химической реакции.

Левая часть уравнения (1.8) отражает общее изменение концентрации исходного вещества во времени в элементарном объеме, для которого составляется материальный баланс. Это накопление вещества А. Левой части уравнения соответствует величина ВАнак. в уравнении баланса (1.7).

Первая группа членов правой части уравнения (1.8) – произведения составляющих скорости потока вдоль осей координат на градиенты концентраций – отражает изменение концентрации А в элементарном объеме вследствие переноса его вместе с самой средой в направлении, совпадающем с направлением общего потока.

Вторая группа членов правой части уравнения (1.8) – произведение Д на сумму вторых производных от концентрации по x, y, z – отражает изменение концентрации А в элементарном объеме в результате переноса его путем диффузии.

Суммарному переносу вещества в движущейся среде конвективным переносом и диффузией соответствует в уравнении (1.7) величине ВАконв (суммарный перенос вещества называют конвективным массообменном или конвективной диффузией).

И, наконец, член rA показывает изменение концентрации А в элементарном объеме за счет химической реакции. Ему в уравнении (1.7) соответствует величина ВАхр.

В зависимости от типа реактора и режима его работы дифференциальное уравнение материального баланса (1.8) упрощается и решение его значительно облегчается.

В том случае, когда параметры процесса постоянны по всему объему реактора и во времени, нет необходимости составлять баланс в дифференциальной форме. Баланс составляют в конечных величинах, беря разность значений параметров на входе в реактор и выходе из него.

Все процессы, протекающие в химических реакторах, делят на:

- стационарные (установившиеся),

- нестационарные (неустановившиеся).

К первым относят процессы, при которых не происходит изменения во времени параметров процесса (например, концентрации А, температуры и т.д.), поэтому в таких реакторах отсутствует накопление вещества (или тепла) и производная от параметра во времени равна нулю. Так, при стационарном режиме для компонента А:

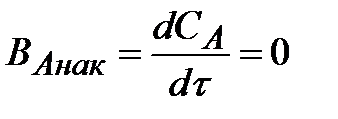
(1.9)

При нестационарных режимах параметры непостоянны во времени и всегда имеется накопление вещества (тепла):

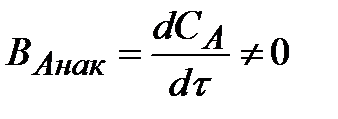
(1.10)

Как уже отмечалось, уравнение материального баланса является исходным при расчете реактора любого типа. Вместе с тем оно не позволяет учитывать тепловой режим в реакторе и влияние температуры на статику и кинетику процесса.

Поэтому при выборе оптимального режима в реакторе, разработке методов его поддержания, расчета реакторов с теплообменной аппаратурой материальный баланс реактора должен решаться совместно с тепловым балансом.

Тепловой баланс, так же как и материальный, может быть составлен в различной форме. Связующим звеном при совместном решении уравнений материального и теплового баланса служит кинетическое уравнение реакции, а также уравнение Аррениуса. Далее будут показаны методы расчета реакторов различных типов. Для этого предварительно дается классификация реакторов.