Исходные положения для расчета реакторов

Разработка реакторов начинается:

- С исследования гидродинамической модели процесса как основы его математического описания.

- Далее изучают кинетику химических реакций,

- процессы массопередачи,

- процессы теплопередачи.

Чем глубже изучена кинетика реакций, тем надежнее предсказания результатов протекания соответствующих процессов.

Кинетические уравнения, записанные в дифференциальной форме, интегрируют по объему реактора. При этом часто возникают трудности, поскольку состав и температура реакционной смеси могут различаться в разных точках реакционного пространства в зависимости от термодинамических характеристик реакций, также от скорости теплообмена с окружающей средой. Кроме того, характер движения жидкости в аппарате, определяемый реальной геометрией реактора, будет влиять на перераспределение вещества и тепла в реакторе.

Поэтому для выбора конструкции и определения размеров любого реактора необходимо принимать во внимание большое число различных факторов и прежде всего располагать следующими данными:

- Величинами, характеризующими скорость протекания химических реакций, а также скорость массопередачи и теплопередачи.

- Внешними ограничениями, накладываемыми технологическим оборудованием, такими, как: модель реактора, которая определяет его гидродинамическую характеристику и скорость процессов переноса вещества и тепла.

Производительность установки (цеха), степень превращения реагентов, концентрацию реагентов и температурный режим устанавливают из ряда теоретических предпосылок.

Нужно учитывать также ряд общих требований к реакторам, которые должны обеспечить:

- Высокую производительность единицы реакционного объема.

- Высокую селективность для сложного процесса.

- Низкие энергетические затраты.

- Простоту обслуживания, дешевизну в изготовлении и выполнение требований техники безопасности.

- Надежность регулирования и устойчивость технологического режима.

- Низкую стоимость продукции.

Приведенные требования несколько противоречивы, поэтому при расчете и конструировании реакторов стремятся найти решения, обеспечивающие в конечном счете общую экономичность процесса.

Одним из важнейших показателей, отражающих совершенство химического реактора, является его интенсивность, которая характеризуется количеством целевого продукта, получаемого в единицу времени при заданных условиях с единицы объема (площади) аппарата. Интенсивность аппарата тем выше, чем меньшее время затрачивают на получение заданного количества продукта.

Поэтому, главной задачей при изучении процессов, протекающих в реакторах любого типа, является установление функциональной зависимости времени пребывания реагентов в реакторе от различных факторов:

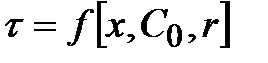,	(1.1)
где x – заданная степень превращения реагента; С0 – начальная концентрация реагента; r – скорость химической реакции.

Уравнение, связывающее четыре названные величины, называется характеристическим уравнением реактора.

Исходным уравнением для получения характеристического уравнения реактора любого типа является материальный баланс, составленный по одному из компонентов реакционной смеси. Составим материальный баланс по исходному веществу А при проведении простой необратимой реакции:

А→R

(1.2)

В общем виде уравнение материального баланса записывается так:

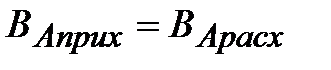,	(1.3)
где ВАприх. – количество вещества А, поступающее в единицу времени в тот реакционный объем, для которого составляется баланс; ВАрасх. – количество вещества А, расходуемое в единицу времени в реакционном объеме.

Учитывая, что поступившее в реактор вещество А расходуется в трех направлениях, можно записать

,	(1.4)
где ВАхр – количество вещества А, вступающее в реакционном объеме в химическую реакцию в единицу времени; ВАст. – сток вещества А (количество вещества А, выходящее из реакционного объема в единицу времени); ВАнак. – накопление вещества А (количество вещества А, остающееся в реакционном объеме в неизменном виде в единицу времени).

С учетом уравнения (1.4) уравнение (1.3) записывается в виде

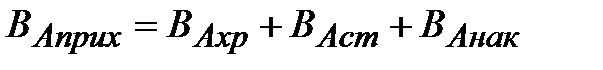
(1.5)

Разность между количеством вещества А, поступающим в единицу времени в реактор (ВАприх.) и выходящим из него (ВАст) – это количество вещества А, переносимое конвективным потоком (ВАконв):_.

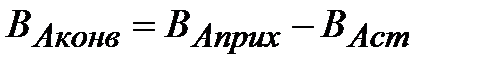
(1.6)

Принимая это во внимание, уравнение (1.5) можно записать еще в одной форме:

(1.7)

В каждом конкретном случае уравнение материального баланса принимает различную форму. Он может составляться для единицы объема реакционной массы либо для реактора в целом. При этом можно рассчитывать материальные потоки, проходящие через объем за единицу времени, а можно относить эти потоки к молю одного из исходных реагентов.

Так, в общем случае, когда состав, температура и другие параметры непостоянны в различных точках реактора или непостоянны во времени, материальный баланс составляют в дифференциальной форме для элементарного объема реактора. В результате получают уравнение конвективного массообмена (А.Г.Касаткин. Основные процессы и аппараты химической технологии, – М: Химия, 1973.), дополненное членом rA, учитывающим протекание химической реакции. Составленное по исходному реагенту А, оно имеет вид:

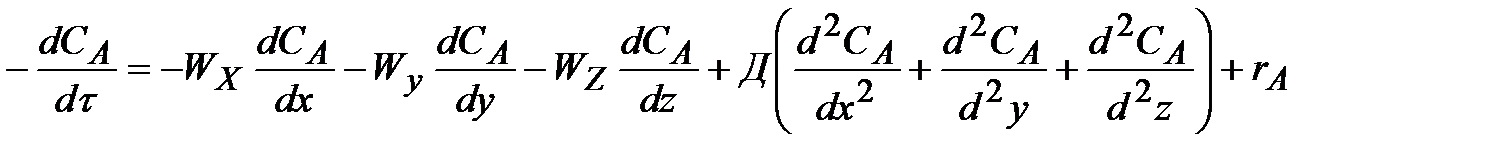,	(1.8)
где CA – концентрация вещества А в реакционной смеси; х, y, z – пространственные координаты; Д – коэффициент молекулярной и турбулентной диффузии; rA – скорость химической реакции.

Левая часть уравнения (1.8) отражает общее изменение концентрации исходного вещества во времени в элементарном объеме, для которого составляется материальный баланс. Это накопление вещества А. Левой части уравнения соответствует величина ВАнак. в уравнении баланса (1.7).

Первая группа членов правой части уравнения (1.8) – произведения составляющих скорости потока вдоль осей координат на градиенты концентраций – отражает изменение концентрации А в элементарном объеме вследствие переноса его вместе с самой средой в направлении, совпадающем с направлением общего потока.

Вторая группа членов правой части уравнения (1.8) – произведение Д на сумму вторых производных от концентрации по x, y, z – отражает изменение концентрации А в элементарном объеме в результате переноса его путем диффузии.

Суммарному переносу вещества в движущейся среде конвективным переносом и диффузией соответствует в уравнении (1.7) величине ВАконв (суммарный перенос вещества называют конвективным массообменном или конвективной диффузией).

И, наконец, член rA показывает изменение концентрации А в элементарном объеме за счет химической реакции. Ему в уравнении (1.7) соответствует величина ВАхр.

В зависимости от типа реактора и режима его работы дифференциальное уравнение материального баланса (1.8) упрощается и решение его значительно облегчается.

В том случае, когда параметры процесса постоянны по всему объему реактора и во времени, нет необходимости составлять баланс в дифференциальной форме. Баланс составляют в конечных величинах, беря разность значений параметров на входе в реактор и выходе из него.

Все процессы, протекающие в химических реакторах, делят на:

- стационарные (установившиеся),

- нестационарные (неустановившиеся).

К первым относят процессы, при которых не происходит изменения во времени параметров процесса (например, концентрации А, температуры и т.д.), поэтому в таких реакторах отсутствует накопление вещества (или тепла) и производная от параметра во времени равна нулю. Так, при стационарном режиме для компонента А:

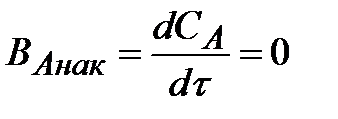
(1.9)

При нестационарных режимах параметры непостоянны во времени и всегда имеется накопление вещества (тепла):

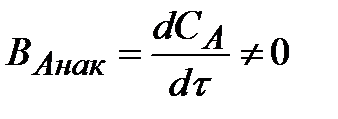
(1.10)

Как уже отмечалось, уравнение материального баланса является исходным при расчете реактора любого типа. Вместе с тем оно не позволяет учитывать тепловой режим в реакторе и влияние температуры на статику и кинетику процесса.

Поэтому при выборе оптимального режима в реакторе, разработке методов его поддержания, расчета реакторов с теплообменной аппаратурой материальный баланс реактора должен решаться совместно с тепловым балансом.

Тепловой баланс, так же как и материальный, может быть составлен в различной форме. Связующим звеном при совместном решении уравнений материального и теплового баланса служит кинетическое уравнение реакции, а также уравнение Аррениуса. Далее будут показаны методы расчета реакторов различных типов. Для этого предварительно дается классификация реакторов.