Уравнение теплового баланса реактора

Тепловой баланс в общем виде можно представить уравнением:

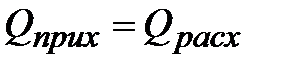,	(3.1)
где Qприх – количество тепла, поступающего в реактор в единицу времени; Qрасх – количество тепла, расходуемое в единицу времени.

Рассмотрим случай, когда простая необратимая реакция (1.2) протекает с выделением тепла, т.е.:

А ® R + Q хр

(3.2)

Тогда приход тепла можно записать в виде:

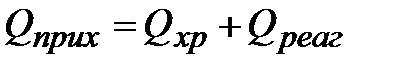,	(3.3)
где Qхр – количество тепла, выделяющееся в результате химического превращения вещества А, в единицу времени; Qреаг – количество тепла, вносимое исходными реагентами, поступающими в реактор, в единицу времени.

Расход тепла может быть представлен уравнением:

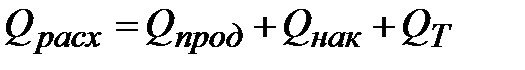,	(3.4)
где: Qпрод – количество тепла, уносимое из реактора продуктами реакции, в единицу времени; Qнак – количество тепла, накапливающееся в реакторе в единицу времени; QТ – количество тепла, расходуемое в единицу времени в результате теплообмена с окружающей средой.

Подставив значения Qприх и Qрасх (3.3 и 3.4) в уравнение, получаем:

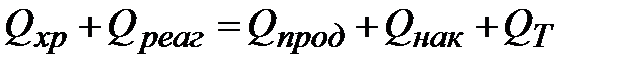
(3.5)

После перестановки членов уравнения (3.5) может быть записано в таком виде:

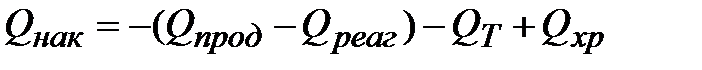
(3.6)

Разность между теплом, уносимым из реактора нагретыми продуктами реакции и теплом, вносимым в реактор исходными реагентами, представляет конвективный поток тепла:

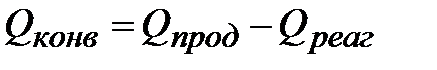
(3.7)

С учетом выражения (3.7) уравнение (3.6) примет вид:

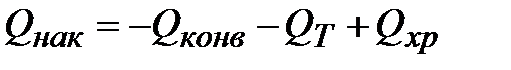
(3.8)

Уравнение теплового баланса (3.8) может принимать различную форму в зависимости от типа реактора и теплового режима процесса.

В общем случае имеет место изменение параметров процесса (температура, концентрация и др.) по объему реактора или по времени, в связи с чем тепловой баланс (так же, как и материальный) составляют в дифференциальной форме.

Для этой цели используют дифференциальное уравнение конвективного теплообмена (А.Г. Касаткин, Основные процессы и аппараты в химической технологии, 1971, стр. 294), в которое вводят дополнительные члены, учитывающие отвод тепла в результате теплообмена) и тепло реакции; с такими дополнениями уравнение имеет вид:

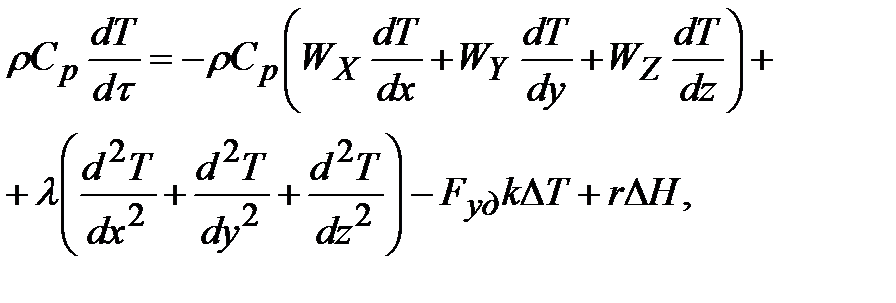
(3.9)

где  – плотность реакционной смеси; Ср – удельная теплоемкость реакционной смеси; x,y, z – пространственные координаты; Wx, Wy, Wz – составляющие скорости движения потока в направлении осей x, y, z;  – коэффициент молекулярной и турбулентной теплопроводности реакционной смеси; Fуд – удельная поверхность теплообмена; K – коэффициент теплопередачи;  T = T – TТ; T – температура реакционной смеси; TТ – температура в теплообменнике; r – скорость химической реакции;  H – тепловой эффект реакции.

Группа членов левой части уравнения (3.9) выражает скорость накопления тепла в элементарном объеме, для которого составляется тепловой баланс. Этому члену соответствует величина Qнак, уравнение (3.8), т.е.:

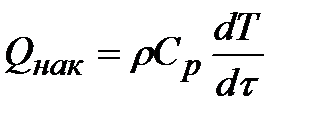
(3.10)

Первая группа членов первой части уравнения (3.9) отражает конвективный перенос тепла по соответствующим координатам (x, y, z) в элементарном объеме.

Вторая группа членов правой части уравнения (3.9) отражает изменение тепла, связанное с теплопроводностью реакционной среды ().

Суммарному переносу тепла конвективным потоком, отражаюшим влияние теплопроводности (обратная диффузия), соответствует в уравнении (3.8) член Qконв, в результате чего можно записать:

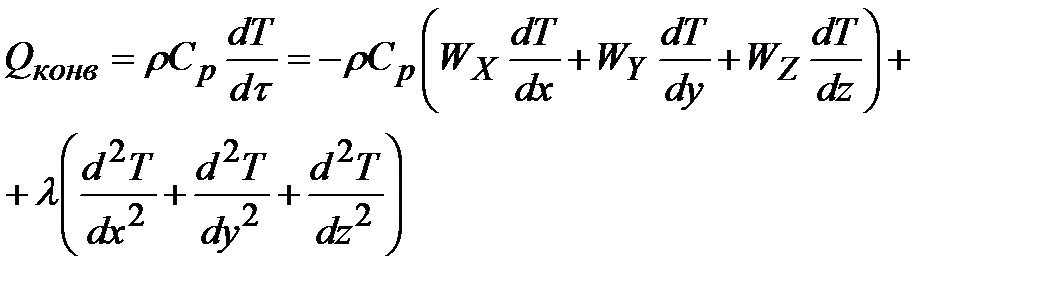
(3.11)

Из сравнения уравнений (3.8) и (3.9) далее следует:

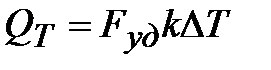
	(3.12)
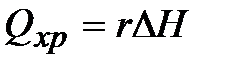
	(3.13)

Решение уравнения (3.9) часто связано с большими трудностями. Однако, как будет показано ниже, в зависимости от характера протекающей реакции, гидродинамического и теплового режимов в реакторе, значение отдельных членов уравнения становится пренебрежительно мало, что приводит к более простым уравнениям, обеспечивающим достаточно точные решения самых разнообразных практических задач.

Уравнения (3.8) и (3.9) представляют математическое описание потоков тепла в нестационарном режиме, когда имеет место накопление тепла и температура процесса меняется во времени.

Для реакторов непрерывного действия характерен стационарный режим. Неустановившееся состояние наблюдается только в пусковой период и в период остановки реактора.

В дальнейшем все реакторы непрерывного действия будут рассматриваться только в стационарном режиме, когда отсутствует накопление тепла, т.е. Qнак = 0.

В реакторах периодического действия режим всегда нестационарный: происходит накопление тепла в результате химического превращения, и температура в любой точке реактора меняется во времени, т.е. Qнак  0.

С другой стороны, в реакторах периодического действия отсутствует конвективный перенос тепла и член Qконв = 0.

Из приведенных примеров следует, что для описания конкретных типов реакторов уравнения (3.8) и (3.9) приобретут более простой вид. Форма уравнения теплового баланса определяется также тепловым режимом в реакторе, что будет показано в дальнейшем.

Ниже даются выводы уравнений тепловых балансов и способы их решения для различных типов реакторов, работающих в различных тепловых режимах.