Периодические реакторы. Реактор идеального смешения периодический

Реакторы периодические характеризуются одновременной и одноразовой загрузкой реагентов. При этом процесс складывается из трех стадий:

- загрузки сырья;

- его обработки (химического превращения);

- выгрузки продукта.

После проведения этих операций они повторяются вновь, т.е. работа реактора осуществляется циклически.

Время одного цикла, проводимого в периодическом реакторе, определяется по уравнению

,	(2.2)
где τn – полное время цикла;  – рабочее время (затрачиваемое на проведение химической реакции); в – вспомогательное время (затрачиваемое на загрузку реагентов и выгрузку продукта).

Реактор идеального смешения периодический – РИС-П – это реактор периодического действия с мешалкой (рис.2.1). Перемешивание в таком реакторе настолько интенсивное, что в каждый данный момент времени концентрация реагентов одинакова по всему объему реактора и меняется лишь во времени, по мере протекания химической реакции.

Периодические процессы по своей природе всегда являются нестационарными, т.к. в них за счет химической реакции происходит изменение во времени параметров процесса, например, концентрации веществ, участвующих в реакции, т.е. имеет место накопление вещества.

Для расчета периодического реактора надо знать его характеристическое уравнение, позволяющее определить рабочее время , необходимое для достижения заданной концентрации вещества CAo и известной кинетике процесса (т.е. известной зависимости скорости химической реакции – rA от концентрации реагентов и температуры).

NAo – начальное количество исходного вещества А в реакционной смеси (при загрузке в реактор); CAo – начальная концентрация вещества А в реакционной смеси; xAo – начальная степень превращения вещества А; NA, CA, xA – то же, в конце процесса;  – время; y – пространственная координата (координата места).

Рис. 2.1 – Реактор идеального смешения периодического действия (РИС-П)

Исходным соотношением для получения характеристического уравнения реактора, как уже говорилось, является уравнение (1.8) материального баланса в дифференциальной форме (дифференциальное уравнение конвективного массообмена).

В РИС-П все параметры (в том числе и концентрация реагента А – СА) одинаковы по всему объему реактора в любой момент времени (так как реакционная смесь интенсивно перемешивается).

Производная любого порядка от концентрации по x, y, z равна нулю, и поэтому можно записать:

,	(2.3)
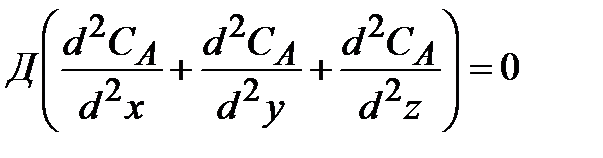
	(2.4)

С учетом полученных значений уравнение (1.8) упрощается и может быть записано не в частных производных, а в виде обыкновенного дифференциального уравнения:

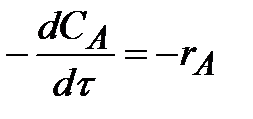
(2.5)

При выражении скорости реакции по исходному веществу А: .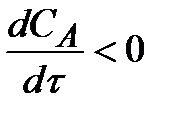

Поэтому, перед 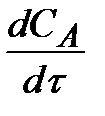и rA ставят знак минус, чтобы скорость являлась положительной величиной.

Изменение концентрации исходного вещества А во времени и по объему для реакции, протекающей в периодическом реакторе идеального смешения, показано на рисунке 2.2.

а – по времени; б – по месту

Рис. 2.2 – Распределение концентрации реагента А в РИС-П

Текущую концентрацию реагента А рассчитывают по уравнению

(2.6)

Все реакции протекают либо без изменения, либо с изменением объема реакционной смеси. Для реакций первого типа (V =const) текущая концентрация реагента А равна

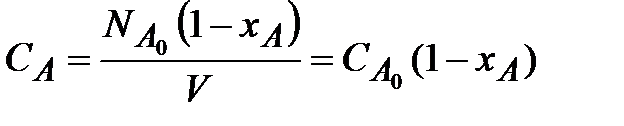
(2.7)

Подставив полученное значение для CA в уравнение (2.5), находим:

(2.8)

или

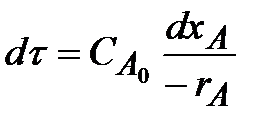
(2.9)

Интегрируя уравнение (2.9) в пределах изменения времени от 0 до  и степени превращения от 0 до хА, получаем характеристическое уравнение РИС периодического действия для условий, когда объем реакционной смеси не изменяется в течение процесса:

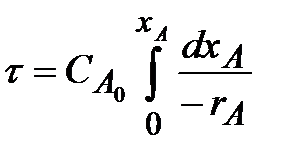
(2.10)

Рассмотрим некоторые частные случаи этого уравнения.

Для необратимой реакции n -го порядка скорость реакции выражается уравнением:

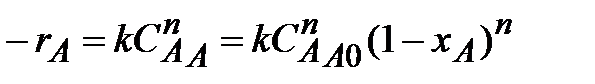
(2.11)

Подставив полученное значение для (- rA) в уравнение (2.10) и учитывая, что константа скорости, k, – величина постоянная в изотермических условиях, получим

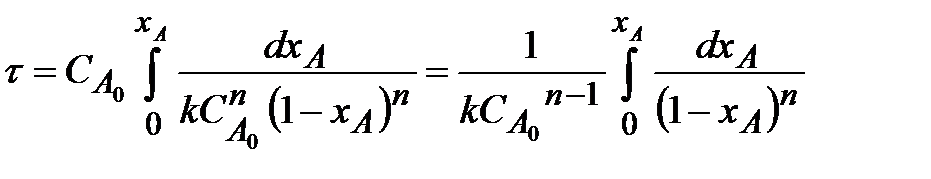
(2.12)

Для необратимой реакции нулевого порядка

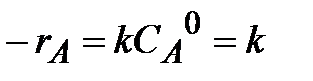
(2.13)

Поэтому, из уравнения (2.10) следует

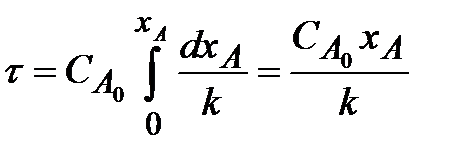
(2.14)

Для необратимой реакции первого порядка

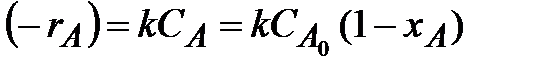
(2.15)

Поэтому подстановкой этого значения в уравнение (2.10) получаем:

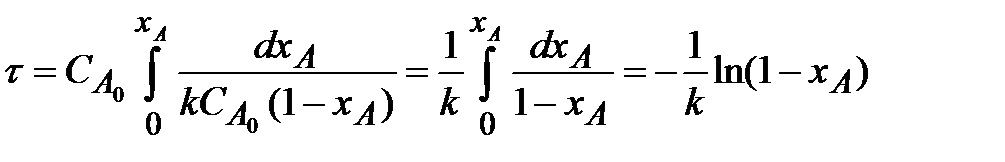
(2.16)

или

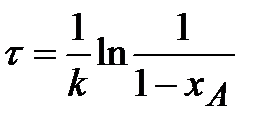
(2.17)

В тех случаях, когда интегрирование уравнения (2.10) связано с трудностями, определение времени  производят методом графического интегрирования. Для этого строят графическую зависимость 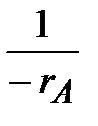от xА и вычисляют площадь под кривой между начальным xAo и конечным xA значениями степени превращения. Для xAo =0 искомая площадь выражается уравнением (рис. 2.3):

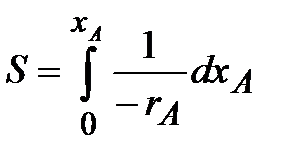
(2.18)

Подставив полученное значение для S в уравнение (2.10), находим:

(2.19)

Приведенная на рисунке 2.1. схема РИС-П является одновременно схемой физической модели этого реактора. Если изготовить такой реактор в малом масштабе (модель промышленного реактора), а затем включить его в работу с поддержанием соответствующего технологического режима, то, исследовав такую модель, можно получить основные данные, необходимые для проектирования промышленных реакторов.

Рис. 2.3 – Графический расчет РИС – П

Исследование состоит в том, что опытные данные представляют в форме зависимостей безразмерных комплексов, составленных комбинацией различных физических величин и линейных размеров. Такая форма представления опытных данных позволяет распространить найденные зависимости на группу подобных между собой явлений, характеризующих постоянством определяющих безразмерных комплексов или критериев подобия (Рейнольдса, Фруда, Архимеда, Пекла, Прандтля, Куссельта и др.). Поэтому, физическое моделирование сводится к воспроизведению постоянства определяющих критериев подобия в модели и в объекте.

Математической моделью РИС-П является его характеристическое уравнение (2.10). Исходя из этого уравнения, представляется возможным определить размеры реактора, а также исследовать эту модель с точки зрения определения оптимальных значений всех параметров, входящих в характеристическое уравнение.

Исследование математической модели обычно проводят на электронно-вычислительной машине (ЭВМ), обладающей большими возможностями в отношении проведения вычислительных операций. Во многих случаях на основе результатов таких исследований представляется возможным вести проектирование промышленного реактора без проведения исследований на опытной установке, при условии достаточно полного изучения кинетики процесса в лабораторных условиях.