Решение. Найдем, например, угол между ребром AS и плоскостью ABC

Найдем, например, угол между ребром AS и плоскостью ABC.

Поскольку AO − проекция AS на плоскость основания и cos∠(AO,AS) = 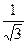, то ∠(AO, AS) = arccos 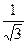. Следовательно, ∠(AS, ABC) = arccos .

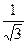Задача 3. В правильной четырехугольной пирамиде SABCD (S – вершина), сторона основания которой равна a, а боковое ребро l, найти расстояние между прямой AB и плоскостью SCD.

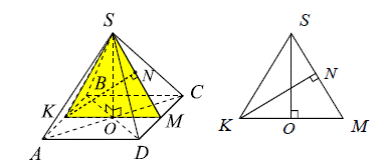Решение. Прямая AB параллельна плоскости SCD (AB||CD). Проведем плоскость через вершину S и середины К и М ребер AB и CD. Эта плоскость перпендикулярна плоскости SCD. Перпендикуляр KN к прямой SM является перпендикуляром и к плоскости SCD. Его длина равна искомому расстоянию. Высоты боковых граней пирамиды равны: 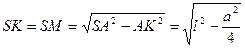, высота 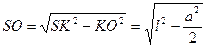. Выражая площадь равнобедренного треугольника SKN двумя способами 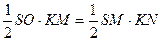, из последнего равенства получаем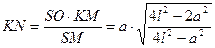

Задача 4.В ромбе АВСD угол А равен 60°, сторона ромба равна 4. Прямая АЕ перпендикулярна плоскости ромба. Расстояние от точки Е до прямой DC равно 4. Найти квадрат расстояния от точки А до плоскости ЕDC.