 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Образец выполнения задания
|
|
Построить графики функции 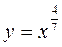 и провести исследование по следующей схеме:
и провести исследование по следующей схеме:
1. Найти область определения функции.
2.Найти множество значений функции.
3.Свойства функции: непрерывность, четность (нечетность), возрастание (убывание), интервалы знакопостоянства.
4. Нули функции.
5.Точки пересечения с осями координат.
6.Периодичность функции.

| x | -1 | -128 | |||
| y |

1. Область определения множество R всех действительных чисел: 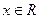 .
.
2. Множество значений функции:  .
.
3. Функция  непрерывна в области определения.
непрерывна в области определения.

4. Функция
5. Функция возрастает на промежутке 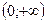 , убывает -
, убывает -  .
.
6. Функция положительна на всей области определения.
7. Нули функции: y = 0 при х = 0.
8. Точка пересечения с осями координат – (0;0).
9. Функция непериодическая.
Выполнить задания:
Построить графики функции и провести исследование по следующей схеме:
1. Найти область определения функции.
2.Найти множество значений функции.
3.Свойства функции: непрерывность, четность (нечетность), возрастание (убывание), интервалы знакопостоянства.
4. Нули функции.
5.Точки пересечения с осями координат.
6.Периодичность функции.


3. Повторная работа над материалом учебника. Построение и преобразование графиков в различных прикладных информационных программах (проектно-исследовательская деятельность).
Ответить на вопросы:
1. Сформулируйте определение функции.
2. Что называется областью определения функции?
3. Что называется областью значения функции?
4. Какими способами может быть задана функция?
5. Какие функции называются четными и как они исследуются на четность?
6. Какие функции называются нечетными и как они исследуются на нечетность?
7. Приведите примеры четных и нечетных функций.
8. Какие функции называются возрастающими и убывающими?
9. Какие функции называются обратными?
10. Перечислите основные элементарные функции?
11. Как связаны между собой графики логарифмической и показательной функций?
12. Как связаны между собой графики функций синуса и арксинуса?
13. Как связаны между собой графики функций косинуса и арккосинуса?
14. Как связаны между собой графики функций тангенса и арктангенса?
Выполнить задания:
Построить графики функций.
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
4. Решение вариантных задач и упражнений.
Выполнить задания:
1. Построить графики функций в среде Mathcad и провести исследование схеме.

2. Найдите функцию, обратную данной, укажите область определения и область значений обратной функции, Постройте графики данной и обратной функции в одной системе координат.
а)  ,
,
б)  ,
,  ,
,
в) 
3. Найдите область определения каждой из функций:
а)  б)
б)  в)
в) 
г)  д)
д) 
4. Построить графики функций:
а)  б)
б)  в)
в)  г)
г) 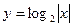
д)  е)
е)  ж)
ж)  з)
з) 
4. Какие из указанных ниже функций являются четными: какие нечетными и какие не являются ни четными, ни нечетными:
а)  ; б)
; б)  ; в)
; в)  .
.
5. Запишите все решения уравнения  , принадлежащие промежутку
, принадлежащие промежутку  .
.
6. Запишите все решения неравенства  , принадлежащие промежутку
, принадлежащие промежутку  .
.
5. Ответы на контрольные вопросы.
Вопросы п.3
Дата публикования: 2015-09-18; Прочитано: 631 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
