Аэродинамические характеристики самолета

В общем случае при полете самолета (при наличии угла атаки α и угла скольжения β) вектор полной аэродинамической силы самолета _a ориентирован в пространстве произвольным образом. В соответствии с записанным ранее выражением для полной аэродинамической силы проекции ее на оси скоростной системы координат можно записать в следующем виде:

; ;

Здесь Y_a - подъемная сила самолета, Н; X_a - сила лобового сопротивления (составляющая силы _a по оси OX_a скоростной системы осей координат, взятая с обратным знаком), Н; Z_a - боковая сила, Н; C_Ya, C_Xa , C_Za - соответственно безразмерные коэффициенты подъемной силы, силы лобового сопротивления и боковой силы; S - площадь крыла самолета, м²; ρ V ²/2 - скоростной напор, Па.
Отсюда

Физический смысл коэффициентов C_Ya, C_Xa, C_Za аналогичен физическому смыслу коэффициента полной аэродинамической силы C_Ra .
Составляющие (C_Ya, C_Xa и C_Za ) безразмерного коэффициента полной аэродинамической силы C_Ra и положение точки ее приложения (центр давления) полностью описывают аэродинамические характеристики самолета.
В установившемся полете без скольжения (β =0) боковая сила отсутствует, поэтому, естественно,

Рис. 5.31. Зависимость аэродинамических коэффициентов от угла атаки (пример)

Рис. 5.32. Поляра самолета (пример)

Обычно принято представлять аэродинамические характеристики самолета в виде зависимостей составляющих коэффициента полной аэродинамической силы (C_Ya и C_Xa) от полетных углов (α и β). Примерные зависимости C_Ya (α) и C_Xa (α) приведены на рис. 5.31.

При достижении критического угла атаки на крыле начинается срыв потока, подъемная сила резко падает. Срыв обычно начинается не одновременно на левой и правой консоли крыла (франц. console - конструкция, жестко закрепленная одним концом при свободном другом).
Это происходит вследствие наличия скольжения, технологических неточностей при изготовлении самолета - возможна "валежка" (резкое кренение самолета). Поэтому в эксплуатации ограничивают диапазон летных углов атаки самолета предельно допустимым углом α_доп, который меньше α_кр на 2-5°.
Одной из форм представления аэродинамических характеристик самолета является поляра - взаимозависимость коэффициентов C_Ya и C_Xa (рис. 5.32). Каждая точка на поляре соответствует определенному углу атаки α.
Обычно при построении поляры принято масштаб для C_Ya брать крупнее, чем для C_Xa.
Если построить поляру в одинаковых масштабах для C_Ya и C_Xa (рис. 5.33), то ее можно рассматривать как полярную диаграмму в координатах C_Ra и φ, где φ - угол наклона полной аэродинамической силы к направлению потока V _¥. В этом случае поляра является геометрическим местом концов вектора коэффициента полной аэродинамической силы . Характерными точками поляры являются:

- угол α_о нулевой подъемной силы (C_Ya =0; C_{X a} = C_Xa0 » C_Xamin);
- наивыгоднейший угол атаки α_нв, соответствующий максимальному аэродинамическому качеству самолета, определенному нами ранее как отношение подъемной силы самолета к силе лобового сопротивления.

При фиксированном угле атаки α _i, соответствующем определенному режиму полета, K_a = Y_a/X_a = C_Ya / C_Xa, т. е. аэродинамическое качество определяется безразмерными коэффициентами аэродинамических сил, учитывающими форму обтекаемого тела, состояние его поверхности и его положение относительно набегающего потока воздуха при заданной скорости полета (M =const). Из рис. 5.33 видно, что аэродинамическое качество определяется как

K_a = Y_a / X_a = tgφ

Рис. 5.33. К объяснению сущности поляры

Максимальному качеству K_{a max} будет соответствовать угол атаки a_нв, полученный как точка касания поляры с прямой, проведенной из начала координат.
Критическому углу атаки α_кр соответствует максимальный коэффициент подъемной силы C_{Ya max}.
Углу атаки α_доп соответствует предельно допустимый

коэффициент подъемной силыC_{Ya доп .}
Ранее отмечалось, что сила индуктивного сопротивления X_{a i} ~ Y_a ², соответственно коэффициент индуктивного сопротивления запишем в виде C_{Xa i} = AC_Ya ², где коэффициент A, характеризующий сопротивление, обусловленное подъемной силой, учитывает влияние формы крыла самолета на скос потока. Естественно, что, чем длиннее крыло, тем меньше будет влияние перетекания потока с нижней поверхности крыла на верхнюю, тем меньше будет скос потока и меньше C_{Xa i}.
Принимая во внимание выражение C_{Xa i} = AC_Ya ², в диапазоне летных углов атаки можно аппроксимировать поляру самолета квадратичной параболой

C_Xa = C_Xa0 + A C_Ya ²

Коэффициент A называют иногда коэффициентом отвала поляры или просто отвалом поляры.

Рис. 5.34. Зависимость аэродинамического качества от угла атаки (пример)

На основании поляры самолета можно построить зависимость аэродинамического качества от угла атаки (рис. 5.34).
Значения аэродинамических коэффициентов существенным образом зависят от скорости (числа М) полета. Для скоростей полета, соответствующих M _¥< M _крит, коэффициент лобового сопротивления C_{Xa о} определяется только силами сопротивления трения и сопротивления давления. Для скоростей полета, соответствующих M _¥ ³ M _крит, к этому сопротивлению добавляется волновое сопротивление.
В общем виде

C_{Xa о} = C_{Xa тр} + C_{Xa д} + C_{Xa в}

где	CXa тр	-	коэффициент лобового сопротивления сил трения;
	CXa д	-	коэффициент лобового сопротивления сил давления;
	CXa в	-	коэффициент волнового сопротивления.

Следовательно, все аэродинамические характеристики самолета должны быть известны не только в диапазоне летных углов атаки, но и во всем диапазоне скоростей (чисел М) полета.
Примерная зависимость аэродинамических коэффициентов для прямого крыла от числа М приведена на рис. 5.35. Здесь коэффициент 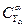- производная коэффициента подъемной силы C_Ya по углу атаки α, 1/рад; 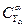= C_Ya /(α - α_о) (см. рис. 5.31).

До чисел М £ 0,4 значения всех аэродинамических коэффициентов практически постоянны, так как сжимаемость воздуха в потоке не проявляется.
С ростом скорости до соответствующей M _крит увеличение коэффициента 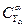происходит из-за проявления сжимаемости и увеличения зоны разрежения над крылом; коэффициент C_{Xa о} медленно растет из-за увеличения зоны повышенного давления перед крылом.

Рис. 5.35. Зависимость аэродинамических коэффициентов прямого крыла от числа М (пример)

В диапазоне чисел М от M _крит до М = 1 увеличение 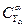замедляется из-за образования местной сверхзвуковой зоны и прямого скачка уплотнения над крылом и достигает максимума к моменту появления местной сверхзвуковой зоны и скачка уплотнения под крылом. С дальнейшим ростом скорости происходит сначала уменьшение до минимума, а затем опять увеличение коэффициента 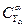, так как смещаются к задней кромке скачки уплотнения сначала на нижней, а затем на верхней поверхности крыла, что сопровождается соответствующим увеличением зон разрежения на этих поверхностях. Увеличение коэффициента 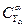прекращается с появлением головного прямого отсоединенного скачка при М =1.
Одновременно резко увеличивается коэффициент лобового сопротивления в связи с развитием волнового кризиса; коэффициент C_{Xa о} достигает максимального значения при М =1 вследствие появления головного прямого отсоединенного скачка.
В диапазоне чисел M >1 с ростом сверхзвуковой скорости головной скачок уплотнения приближается к передней кромке, приобретая форму косого, затем скачок становится присоединенным, углы наклона скачков уменьшаются, соответственно уменьшаются зоны возмущений на верхней и нижней поверхностях профиля, что приводит к уменьшению коэффициентов 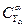и C_{Xa о}.
Резкое увеличение лобового сопротивления (рис. 5.35, 5.36) и, соответственно, уменьшение качества самолета (рис. 5.37) требуют для полета со скоростями, соответствующими M > M _крит (преодоления так называемого "звукового барьера"), значительного увеличения тяги двигателя P.
Напомним, что для совершения горизонтального полета необходимо выполнить условия:

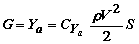
Отсюда потребная для горизонтального полета тяга двигателя

Самолеты с прямым крылом и поршневыми двигателями с воздушными винтами не могли не только достигнуть скоростей полета, соответствующих M ³1, но даже и приблизиться к таким скоростям.

Рис. 5.36. Зависимость максимального аэродинамического качества от числа М и конфигурации крыла самолета (пример)	Рис. 5.37. Зависимость коэффициента лобового сопротивления от числа М и конфигурации самолета (пример)

Рис. 5.36 и 5.37 достаточно наглядно показывают, что выбор соответствующих форм самолета позволяет существенным образом снизить неблагоприятное влияние сжимаемости при полете на высоких скоростях.
Приблизиться к "звуковому барьеру", а затем и преодолеть его стало возможным в связи с созданием реактивных двигателей и разработкой аэродинамиками и конструкторами новых форм самолета.

Глава 6
ОСНОВЫ ДИНАМИКИ ПОЛЕТА САМОЛЕТА