Элементы аэродинамики больших скоростей

Ранее рассматривалось обтекание тел потоком воздуха при скоростях (числах М), на которых сжимаемость воздуха практически не проявляется. С увеличением скоростей полета (чисел М) сжимаемость воздуха существенным образом изменяет картину обтекания. Это связано с особенностями распространения возмущений при сверхзвуковых течениях.

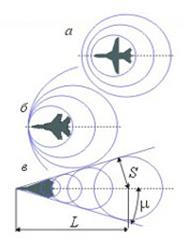
Рис. 5.20. Мгновенная картина сферических волн возмущения

Если самолет, каждая точка которого является источником слабых возмущений, распространяющихся во все стороны со скоростью звука в виде колебаний давления и плотности воздуха, летит с дозвуковой скоростью (рис.5.20, а), сферические волны возмущений опережают самолет, т. е. все пространство вокруг летящего самолета является возмущенным.
При полете самолета со скоростью, равной скорости звука (рис. 5.20, б), созданные самолетом сферические волны возмущений, имеющие также скорость звука, не могут оторваться от источника возмущений и уйти вперед. Они будут накладываться одна на другую и, имея с самолетом общую точку касания, создадут перед ним плоскую поверхность, на которой все звуковые волны находятся в одной фазе колебаний - фазе уплотнения. Эта поверхность разделяет пространство на две области - невозмущенную перед самолетом и возмущенную за ним.
При сверхзвуковой скорости полета самолета (рис. 5.20, в) сферические волны возмущений будут отставать от источника, граница возмущений будет проходить на конической поверхности, называемой конусом возмущений или волной Маха. Угол между образующей этого конуса (линией Маха) и направлением скорости полета называется углом Маха. Его значение определяется отношением пути s=at, пройденного волной возмущения со скоростью звука a за определенный промежуток времени t, к пути

L = Vt, пройденному за это же время самолетом, летящим со скоростью V:

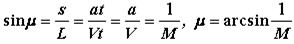
На поверхности конуса Маха, следовательно, будет происходить наложение волн возмущения, находящихся в фазе уплотнения. Поверхность конуса Маха разделяет пространство вокруг летящего самолета на две области - возмущенную внутри конуса и невозмущенную вне его.
Отличительной особенностью именно сверхзвуковых потоков является то, что в сверхзвуковом потоке конусы возмущений (слабые возмущения от множества точечных источников возмущений) накладываются друг на друга и, суммируясь, создают более сильное возмущение среды - ударную волну.
Ударная волна, перемещаясь во все стороны, как бы "останавливается" набегающим потоком, и скорость ее распространения сравнивается со скоростью набегающего сверхзвукового потока. Такая "остановленная" набегающим сверхзвуковым потоком ударная волна называется скачком уплотнения.
Таким образом, в непосредственной близости от обтекаемого потоком тела скачок уплотнения, возникший на передних кромках обтекаемого тела (самолета), является границей возмущений, вызванных телом. По мере удаления от тела скачок уплотнения переходит в волну Маха.

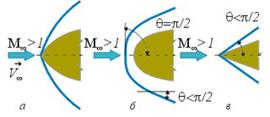
Рис. 5.21. Формы головных скачков уплотнения

В зависимости от значения сверхзвуковой скорости полета и формы головной части тела скачок уплотнения, возникший на передних кромках, может иметь различную форму (рис. 5.21).
В общем случае скачок уплотнения имеет криволинейную форму. Присоединенный криволинейный скачок (рис. 5.21, а) образуется при обтекании заостренного тела. Отсоединенный криволинейный скачок (рис. 5.21, б), который в передней своей части с достаточным приближением может рассматриваться как прямой скачок (q = p/2), образуется при обтекании затупленного тела. По мере удаления от тела он переходит в косой скачок (q <p/2), а затем в волну Маха. Заметим, что угол наклона скачка уплотнения q несколько больше угла наклона линии Маха µ. При сверхзвуковом обтекании заостренного тела с прямолинейными образующими может возникнуть присоединенный прямолинейный скачок уплотнения (рис. 5.21, в).

Рис. 5.22. Изменение параметров потока в скачке уплотнения

Скачок уплотнения (рис. 5.22) можно рассматривать как слой весьма малой толщины d (d =10^-5¸10^{-6 см, т. е. порядка длины свободного пробега молекул), "натолкнувшись" на который сверхзвуковой поток теряет часть своей кинетической энергии в результате преобразования ее в энергию давления и тепловую энергию. Одновременно с резким уменьшением скорости от V} ₁ до V ₂ в скачке происходит резкое (скачкообразное) повышение давления (p ₂> p ₁), плотности (r₂> r₁) и температуры (T ₂> T ₁).

Установлено, что переход от сверхзвуковой скорости V ₁ к дозвуковой V ₂ всегда происходит только в прямом скачке уплотнения (рис. 5.22, а). В косом скачке (рис. 5.22, б) качественно параметры потока меняются так же, как в прямом, но интенсивность изменения параметров меньше, и за косым скачком вектор скорости потока изменяет направление 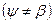, а скорость V ₂ может оставаться сверхзвуковой. Процессы, происходящие в скачках, необратимы, так как часть тепла, выделяющаяся при нагревании воздуха в скачке, рассеивается в окружающем пространстве. Поскольку интенсивность косых скачков уплотнения меньше, чем прямых, потери энергии в косом скачке меньше. Потери энергии в скачке уплотнения являются дополнительным источником сопротивления.

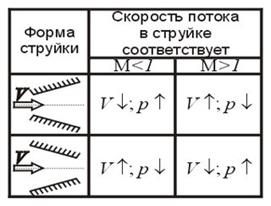
Рис. 5.23. Изменение параметров потока в струйке

Явления, связанные с возникновением ударных волн и скачков уплотнения, называются волновым кризисом.

Свойства сжимаемости воздуха на больших скоростях полета приводит к тому, что изменение параметров сверхзвукового потока (скорости V и давления р) в струйке коренным образом отличается от дозвукового потока (рис. 5.23). Так, при движении потока сжимаемого газа со сверхзвуковой скоростью в суживающемся канале скорость потока убывает (V ↓), а давление растет (p ↑). Это никоим образом не противоречит выводам, сделанным ранее на основании уравнения неразрывности и уравнения Бернулли. Если не упрощать модель течения, как мы сделали это ранее, приняв плотность газа постоянной, мы из этих уравнений получим результаты, отраженные на рис. 5.23.

Явления волнового кризиса проявляются уже на больших дозвуковых (критических) скоростях полета. На поверхности обтекаемого тела местная скорость потока V _м, увеличиваясь с ростом скорости полета V _¥ (M _¥), может достигнуть местной a _м скорости звука в потоке. На поверхности самолета, летящего с дозвуковой скоростью (M _¥<1), возникают зоны потока с местными скоростями M _м, равными скорости звука и превышающими ее (M _м ³1).

Рис. 5.24. К возникновению волнового кризиса

Скорость полета самолета V _¥ (M _¥), при которой где-либо на поверхности самолета местная скорость обтекания становится равной местной скорости звука, называется критической скоростью V_крит (M _крит). Естественно, что M _крит <1.

В струйке, обтекающей профиль крыла (рис. 5.24), площади поперечных сечений по потоку сначала уменьшаются (от сечения I-I до сечения II-II), а затем увеличиваются.
При критической скорости полета в критическом (наименьшем) сечении II-II достигается местная скорость V _м, равная местной скорости звука a _м, и далее вниз по потоку в расширяющейся струйке скорость потока продолжает нарастать. На поверхности профиля появляется местная сверхзвуковая зона (между сечениями II-II и III-III), которая в сечении III-III замыкается местным прямым скачком уплотнения. Скорость потока за скачком становится дозвуковой и далее по потоку уменьшается, сравниваясь за крылом (в сечении IV-IV) с дозвуковой скоростью набегающего потока V _¥. Таким образом, в общем дозвуковом потоке, обтекающем самолет, появляются зоны сверхзвуковых течений и возникают явления волнового кризиса.

При достижении критических скоростей полета изменяется спектр обтекания, на эпюре давлений (рис. 5.25) появляется резкое скачкообразное повышение давления (скачок уплотнения), возникает срыв потока из-под скачка (волновой срыв), ухудшаются несущие способности крыла, центр давления смещается назад по потоку, появляется дополнительное лобовое сопротивление, связанное с необратимыми потерями энергии в скачке. Это дополнительное лобовое сопротивление называют волновым сопротивлением.

Рис. 5.25. Эпюры распределения давления: 1 - при докритических скоростях полета; 2 - при закритических скоростях полета

С увеличением скорости полета скачки уплотнения появляются на нижней поверхности крыла, далее они сдвигаются к задней кромке, при достижении сверхзвуковой скорости скачки "садятся" на передние кромки несущих и ненесущих поверхностей.
На передних кромках в точках полного торможения потока (критических точках), где вся кинетическая энергия превращается в потенциальную энергию давления потока (скоростной напор rV ²/2 трансформируется в статическое давление p), давление и температура будут наибольшими.
Температуру торможения T _т и давление p _т в критической точке можно рассчитать по формулам:

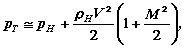
где	T т	-	температура воздуха в точке торможения, К;
	TH	-	температура воздуха на данной высоте, К;
	V	-	скорость полета, м/с;
	aH	-	скорость звука на данной высоте, м/с;
	r H	-	плотность воздуха на данной высоте, кг/м3;
	p T	-	давление воздуха в точке торможения, Па;
	pH	-	давление воздуха на данной высоте, Па.

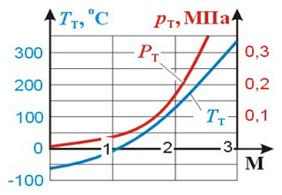
Зависимость параметров потока в точке торможения от числа М полета самолета в стра

Рис. 5.26. Зависимость параметров потока в точке торможения от числа М

тосфере (Н ³11000 м) представлена на рис. 5.26. Повышение температуры воздуха вследствие торможения, а также трения в пограничном слое приводит к сильному кинетическому нагреву конструкции самолета, что требует от конструктора обеспечения нормальных условий для экипажа и пассажиров. Так, при полете в стратосфере со скоростями, превышающими скорость звука (М >1), требуется охлаждение кабины, в то время как полет с дозвуковыми скоростями требует обогрева кабины. Кинетический нагрев усложняет работу силовой установки самолета и различных систем, влияет на прочность конструкции. Высокое давление на носовых частях обтекаемых поверхностей предъявляет особые требования к прочности этих частей.