Основные законы аэродинамики

При реальном полете самолета непрерывно изменяются скорость и другие параметры воздушного потока, обтекающего самолет. Соответственно изменяются и спектры обтекания, и эпюры распределения давления по поверхности самолета. Такое движение называется неустановившимся. Для создания теоретической модели явления введем упрощения, которые позволят нам выяснить основные закономерности, упростят выводы, не снижая, однако, их практического, инженерного значения.
Упрощение первое. Будем рассматривать только установившеесядвижение - такое движение воздушного потока, в каждой точке которого параметры (V - скорость, p - давление, ρ - плотность) не меняются с течением времени.
Упрощение второе. Примем так называемую гипотезу сплошности, или неразрывности, среды. Не будем учитывать молекулярные движения воздуха и межмолекулярные промежутки, т. е. будем рассматривать воздух как сплошную неразрывную среду с определенной плотностью ρ, которая, однако, может изменяться за счет изменения "плотности упаковки" молекул воздуха, имеющих ничтожно малый объем.
Упрощение третье. Будем считать, что вязкость воздуха равна нулю, т. е. нет сил внутреннего трения. Это значит, что из спектра обтекания тела мы удалили пограничный слой, пренебрегли силой лобового сопротивления, обусловленного трением воздуха о поверхность самолета. В дальнейшем, при описании аэродинамических характеристик самолета, учесть эти силы нам позволит специальный раздел аэродинамики - теория пограничного слоя.

В соответствии с принятыми упрощениями можно рассматривать движение струйки неразрывной невязкой среды (идеального сжимаемого газа) внутри трубки тока (рис. 5.14), образованной неизменными во времени траекториями частиц воздуха, проходящими по границе струи.

Рис. 5.14. К выводу основных уравнений аэродинамики

Уравнение неразрывности является математическим описанием закона сохранения материи для струйки идеального сжимаемого газа.
Через сечение струйки I-I внутрь трубки тока за время dt войдет столбик газа объемом F ₁ V ₁ dt, где F ₁ - бесконечно малая площадь столбика (площадь поперечного сечения струйки), м²; V ₁ - скорость потока газа на входе в сечение, м/с; V ₁ dt - длина столбика, м. Секундный массовый расход газа m_{1 cек} = ρ ₁ V ₁ F ₁ - масса газа, прошедшего за одну секунду через сечение струйки I-I, кг/с, где ρ ₁ - плотность газа, кг/м³; V ₁ F ₁ - секундный объемный расход газа, м³/с. В соответствии с гипотезой неразрывности через сечение струйки II-II из трубки тока за одну секунду выйдет масса газа m_{2 cек} = ρ ₂ V ₂ F ₂, равная массе газа m_{1 cек}, вошедшей в трубку тока через сечение I-I. Таким образом, секундный массовый расход газа через любое сечение струйки есть величина постоянная:

ρ VF = const.

Это соотношение называется уравнением неразрывности или уравнением постоянства расхода. При движении самолета с малыми дозвуковыми скоростями V, соответствующими числам M £0,4¸0,6 (конкретное значение M= V/a зависит от формы обтекаемого тела), сжимаемость воздуха практически не проявляется, т. е. можно считать, что плотность воздуха постоянна (ρ = const). В этом случае для струйки ρ₁=ρ₂ и уравнение неразрывности примет вид

VF = const.

Отсюда следует, что для несжимаемого идеального газа скорость в струйке V тем больше, чем меньше площадь сечения струйки F, и наоборот.
Уравнение Бернулли является математическим описанием закона сохранения энергии для струйки идеального сжимаемого газа:

E ₁ = E ₂ =... = const,

т. е. внутри трубки тока, когда нет обмена массой и энергией между струйкой и окружающей ее средой (соседними струйками), сумма всех видов энергии в любом сечении струйки постоянна.
Учитывая только кинетическую энергию и энергию силы давления в струйке, можно записать для любого сечения струйки:

E_i = E _к + E _p,

где	Ei	-	полная энергия в i-м сечении струйки, Дж;
	E к	-	кинетическая энергия движущегося через сечение газа;
	E p	-	энергия силы давления газа.

Кинетическая энергия характеризует способность движущегося газа производить работу:

Энергия силы давления характеризует способность газа производить работу силой давления, проталкивающей газ через сечение струйки:

E_p = PL,

где	P = pF	-	сила давления, Н;
	p	-	давление газа в сечении струйки, Па;
	F	-	площадь поперечного сечения струйки, м2;
	L = Vdt	-	перемещение данного объема газа со скоростью V за промежуток времени dt, м.

Отсюда

С учетом этих выражений запишем уравнение Бернулли в виде

В соответствии с уравнением неразрывности массовый расход m _cек dt = сonst.
Для идеального несжимаемого газа ρ = сonst.
Поэтому для идеального несжимаемого газа уравнение Бернулли запишем в виде

где	ρV 2/2	-	скоростной напор (динамическое давление), Па;
	p	-	статическое давление, Па.

Для идеального несжимаемого газа сумма скоростного напора и статического давления в струйке есть величина постоянная, т. е. с увеличением скорости V давление в струйке p падает, и наоборот.

Рис. 5.15. К построению математической модели картины обтекания

Знание основных законов аэродинамики позволяет построить математическую модель картины обтекания тела свободным потоком (без учета пограничного слоя) и определить значения аэродинамических сил, зависящих от распределения давления по поверхности тела. Если рассмотреть движение (рис. 5.15) частиц газа 1, 2, 3 в различных струйках потока, обтекающего тело, то, в силу гипотезы неразрывности, эти частицы в любой момент времени должны одновременно проходить различные сечения потока сечения (I-I, II-II, III-III). Частица 3 движется в струйке, на которой не сказывается присутствие в потоке тела, поэтому скорость ее в любом сечении V ₃ и давление в струйке p ₃ будут равны скорости V _¥ и давлению в струйке p _¥ невозмущенного потока. Частицы 1 и 2, движущиеся в искривленных струйках по криволинейным траекториям, должны преодолевать более длинный путь, чем частица 3, и, следовательно, двигаться с большими увеличение местными скоростями обтекания, т. е. V ₁ > V _¥; V ₂ > V _¥.
В соответствии с уравнением Бернулли увеличение местных скоростей обтекания приведет к снижению давления в струйке, т. е. p ₁ < p _¥; p ₂ < p _¥.
Зная форму обтекаемого тела, мы может рассчитать траектории движения частиц, определить изменения площади струек вдоль тела. По уравнению неразрывности вычислим местные скорости обтекания и по уравнению Бернулли - распределение давления по поверхности тела.
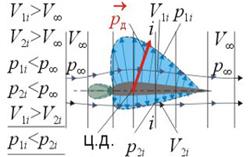
Расчетные методики, построенные на базе основных законов аэродинамики, позволяют достаточно точно описать картины обтекания тел, полученные в результате эксперимента. Очевидно, что для симметричного профиля, обтекаемого потоком воздуха под нулевым углом атаки, характер течения струй, их площади и местные скорости обтекания в i -х сечениях на верхней поверхности V _{1 i} и на нижней поверхности V _{2 i} будут одинаковы. В этом случае для параметров потока (V и p) в соответствии с уравнением Бернулли справедливы соотношения, представленные на рис. 5.16. При несимметричном обтекании на малых углах атаки на основании уравнения Бернулли получим соотношения, представленные на рис. 5.17.
Для каждого i-го сечения значения местных скоростей обтекания профиля можно записать в виде

,

где		-	скорость набегающего потока;
		-	приращение скорости, зависящее от формы траектории движения частиц воздуха вдоль профиля, обусловленной его формой.
	Рис. 5.16. Соотношения, полученные из уравнения Бернулли при симметричном обтекании	Рис. 5.17. Соотношения, полученные из уравнения Бернулли при несимметричном обтекании

Распределение скоростей при несимметричном обтекании профиля (рис. 5.18) сходно с распределением скоростей при вихревом движении.

Рис. 5.18. "Вихревое движение" при обтекании профиля

Н.Е. Жуковский, разработавший в 1906 году теорию подъемной силы крыла, предложил моделировать крыло вихрем, при взаимодействии которого с плоскопараллельным набегающим потоком скорости их суммируются. На верхней поверхности вихря скорость частиц увеличивается (), на нижней - уменьшается (). Значение возникающей при этом подъемной силы зависит от интенсивности вихря, которая измеряется так называемой циркуляцией скорости Г профиля крыла

Г = ΣΔ V_ids,

где ds - элементарная длина соответствующего участка контура.
Н.Е. Жуковский вывел теоретическую формулу для определения подъемной силы для части длиной l крыла бесконечного размаха:

Y_a = ρ V_¥ l Г,

где	Ya	-	подъемная сила, Н;
	ρ	-	плотность воздуха, кг/м3;
	V¥	-	скорость потока, м/с;
	l	-	длина части крыла, м;
	Г	-	циркуляция скорости профиля крыла, м2/с.

Н.Е. Жуковский и С.А. Чаплыгин первыми теоретически установили связь между формой профиля, углом атаки и возникающей вокруг профиля циркуляцией.
Таким образом, простейшие математические модели, описывающие обтекание тела идеальным газом, позволяют нам рассчитать составляющую полной аэродинамической силы - силу давления 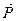_давл, возникающую в результате преобразования кинетической энергии потока (скоростного напора ρV ²/2) в энергию давления (статическое давление p).
В инженерных аэродинамических расчетах принято выражать полную аэродинамическую силу R _a формулой

Здесь	Ra	-	полная аэродинамическая сила, Н;
	CRa	-	безразмерный коэффициент полной аэродинамической силы;
	ρV 2/2	-	скоростной напор, Па;
	S	-	характерная площадь обтекаемого тела, м2.

Полная аэродинамическая сила прямо пропорциональна кинетической энергии потока, которая при обтекании тела трансформируется в энергию трения в пограничном слое и в потенциальную энергию давления.