ОЛДУ и НЛДУ второго порядка с постоянными коэффициентами

Рассмотрим НЛДУ второго порядка с постоянными коэффициентами

. (1)

Соответствующее ему ОЛДУ есть

. (2)

Характеристическое уравнение ОЛДУ (2) есть квадратное уравнение

. (3)

Возможны три случая.

Случай 1: Тогда уравнение (3) имеет два различных действительных корня и Поэтому общее решение ОЛДУ (2) имеет вид

Случай 2: Тогда уравнение (3) имеет один действительный корень кратности 2. В этом случае общее решение ОЛДУ (2) имеет вид

Случай 3: Тогда корнями уравнения (3) будут

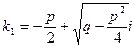и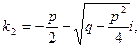

т.е. Следовательно, общее решение ОЛДУ (2) имеет вид

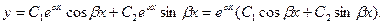
Согласно сводной таблице:

I. Если правая часть уравнения (1) есть то:

a) при частное решение надо искать в виде

b) при частное решение надо искать в виде

c) при частное решение надо искать в виде

II. Пусть правая часть уравнения (1) есть Тогда:

a) если не является корнем характеристического уравнения (3), то частное решение надо искать в виде

b) если является корнем характеристического уравнения (3) кратности 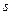, то частное решение надо искать в виде

III. Пусть правая часть уравнения (1) есть Тогда:

a) если (корни характеристического уравнения (3) действительны), частное решение надо искать в виде , где

b) если (уравнение (3) не имеет действительных корней), то для или , но частное решение надо искать в виде , где

c) если (уравнение (3) не имеет действительных корней), то для и частное решение надо искать в виде , где

IV. Пусть правая часть уравнения (1) есть Тогда:

a) если (корни характеристического уравнения (3) действительны), частное решение надо искать в виде , где

b) если (характеристическое уравнение (3) не имеет действительных корней), то для

частное решение надо искать в виде , где

c) если (характеристическое уравнение (3) не имеет действительных корней), то для

или

частное решение надо искать в виде , где

Пример 1. Решить уравнение y'' – 2y' + y = .

Решение. Характеристическое уравнение данного уравнения есть Число 1 есть корень кратности 2. Других корней нет. Фундаментальная система соответствующего однородного уравнения есть . Для нахождения частного решения воспользуемся таблицей (пункт II b)). Частное решение ищем в виде . Имеем

Подставляя в уравнение, получим 2A = , откуда A= . Общее решение уравнения есть y = +