Уравнения в полных дифференциалах

Допустим, что левая часть дифференциального уравнения

(1)

является полным дифференциалом некоторой функции :

.

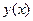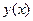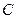Тогда если есть решение дифференциального уравнения (1), то , откуда следует, что . Обратно, если дифференцируемая функция такова, что при некотором , то 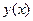есть решение дифференциального уравнения (1). Следовательно,

есть общий интеграл дифференциального уравнения (1). Если даны начальные условия 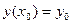, то 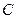определяется равенством , и является искомым частным интегралом.

Для того чтобы выражение было полным дифференциалом некоторой функции, необходимо и достаточно (для ), чтобы . Поэтому уравнение с разделенными переменными есть уравнение в полных дифференциалах.

Уравнение в полных дифференциалах легко интегрируется. Действительно, если

, то .

Пусть . Тогда . Для определения функции дифференцируем это равенство по 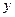и получаем

Из полученного уравнения определяем и, интегрируя, находим .

Пример1. Найти общий интеграл уравнения

. (2)

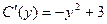Решение. Так как , это уравнение является уравнением в полных дифференциалах. Имеем , откуда . Тогда . Следовательно, , и, тем самым, . Значит

. Таким образом, общий интеграл дифференциального уравнения (2) есть .