Однородные дифференциальные уравнения первого порядка

Определение 1. Функция называется однородной функцией нулевого измерения, если

Полагая 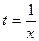, получаем .

Определение 2. Дифференциальное уравнение вида называется однородным, если есть однородная функция нулевого измерения.

Из сказанного выше следует, что однородное уравнение можно записать в виде .

Всякое однородное уравнение подстановкой приводится к уравнению с разделяющимися переменными:

Если есть корень уравнения то решением уравнения будет , а исходного - 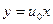. Решения, отличные от 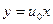, где есть корень уравнения получаются разделением переменных в уравнении .

Определение 3. Мы будем говорить, что есть однородная функция измерения 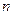, если .

Если дифференциальное уравнение записать в виде где и 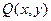- однородные функции одного измерения, то оно приводится к однородному дифференциальному уравнению

.

Дифференциальное уравнение

приводится к однородному в том случае, когда . Действительно, пусть 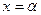и удовлетворяют системе уравнений

.

Положим 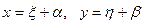. Тогда

, а уравнение 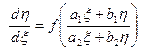однородное.

Пример 1. Проинтегрировать уравнение

Решение. Положим Тогда , и тем самым

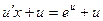или

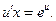(1)

Для данного уравнения поэтому разделив правую и левую части уравнения (1) на , мы получим уравнение или

. (2)

Интегрируя (2), получаем , откуда

Пример 6. Найти частное решение дифференциального уравнения

(3)

удовлетворяющее начальному условию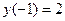

Решение. Мы ищем решение в окрестности точки поэтому можем считать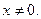

Запишем уравнение (3) в виде

. ()

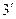Применим подстановку . Получаем или . Следовательно,

Подставляя в последнее равенство , получаем , откуда . Таким образом, .