 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Понятие интегральной суммы, предела интегральных сумм, интеграла Римана
|
|
Определение 1. Рассмотрим отрезок 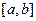 . Набор точек
. Набор точек 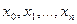 таких, что
таких, что 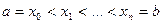 будем называть разбиением отрезка
будем называть разбиением отрезка 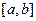 и обозначать, например, через
и обозначать, например, через 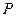 . Отрезки
. Отрезки 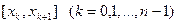 будем называть отрезками разбиения
будем называть отрезками разбиения 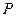 . Диаметром разбиения
. Диаметром разбиения 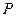 назовем число
назовем число 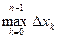 , где
, где  .
.
Условимся диаметр разбиения 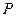 обозначать символом
обозначать символом  .
.
Определение 2. Пусть  ,
,  -разбиение отрезка
-разбиение отрезка 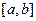 . Для каждого
. Для каждого 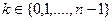 на отрезке
на отрезке  фиксируем произвольную точку
фиксируем произвольную точку 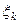 . Сумма
. Сумма 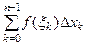 называется интегральной суммой и обозначается
называется интегральной суммой и обозначается  .
.
Определение 3. Число 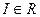 называется пределом интегральных сумм
называется пределом интегральных сумм  при условии, что диаметр
при условии, что диаметр  разбиения
разбиения 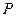 стремится к нулю, если
стремится к нулю, если 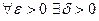 :
: 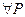 ,
, 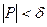 неравенство
неравенство 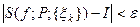 справедливо при любом выборе точек
справедливо при любом выборе точек 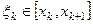
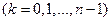 .
.  обозначают
обозначают  .
.
Определение 3. Функция  называется интегрируемой на отрезке
называется интегрируемой на отрезке 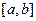 , если существует предел I интегральных сумм
, если существует предел I интегральных сумм  при условии, что диаметр
при условии, что диаметр  разбиения
разбиения 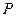 стремиться к нулю. При этом
стремиться к нулю. При этом  называют определенным интегралом (интегралом Римана) на отрезке
называют определенным интегралом (интегралом Римана) на отрезке 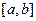 и обозначают
и обозначают  .
.
Предложение 1. Интегрируемая на отрезке 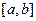 функция необходимо ограничена на
функция необходимо ограничена на 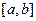 .
.
Предложение 2. Если функция 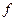 интегрируема на отрезке
интегрируема на отрезке 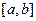 , то
, то
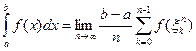 , где
, где 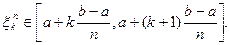
Следствие 1. Если функция 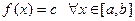 , то
, то 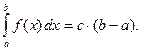
Теорема 1. Если функция 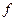 интегрируема на отрезке
интегрируема на отрезке 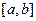 , то функция
, то функция 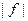 также интегрируема на отрезке
также интегрируема на отрезке 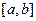 .
.
Дата публикования: 2015-09-18; Прочитано: 790 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
