Интегралы от иррациональных функций

1. Рассмотрим интеграл , где рациональная функция своих аргументов.

Пусть общий знаменатель дробей . Сделаем замену: . Тогда каждая дробная степень выразится через целую степень и, следовательно, подынтегральная функция преобразуется в рациональную функцию от .

2. Интегралы вида сводятся к интегралу от рациональной функции с помощью подстановки , где общий знаменатель дробей .

3. Интегралы от дифференциальных биномов 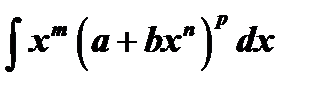, где рациональные числа выражаются через конечную комбинацию элементарных функций в следующих трех случаях:

а) если целое число;

б) если целое число, с помощью подстановки , где знаменатель дроби ;

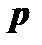в) если целое число, с помощью подстановки .