Площади плоских фигур

Если непрерывная кривая задана в прямоугольных координатах уравнением , то площадь криволинейной трапеции, ограниченной этой кривой, двумя вертикалями в точках и и отрезком оси абсцисс 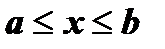(рис.1), определяется формулой

В общем случае, если площадь ограничена двумя непрерывными кривыми и и двумя вертикалями и , где при (рис.2), то будем иметь:

Если кривая задана уравнениями в параметрической форме , то площадь криволинейной трапеции, ограниченной этой кривой, двумя вертикалями, соответствующими и , и отрезком оси , выражается интегралом

,

где и определяются из уравнений и на отрезке .

Если непрерывная кривая задана в полярных координатах уравнением , то площадь сектора (рис.3), ограниченного дугой кривой и двумя полярными радиусами и , соответствующими значениям и , выразится интегралом