Обратная матрица. Пусть имеется невырожденная квадратная матрица го порядка

Пусть имеется невырожденная квадратная матрица 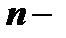го порядка

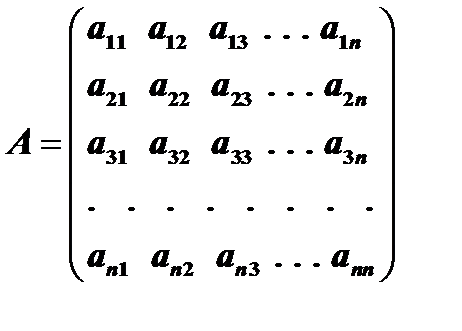, (2)

т.е. матрица, у которой определитель не равен нулю.

Обратной для данной матрицы вида (2) называется матрица 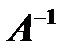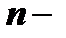го порядка, если произведение матрицы 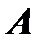на матрицу равно единичной матрице 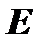, т.е. если

.

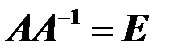Присоединенной матрицей 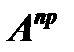к данной матрице (1) называется матрица, составленная из алгебраических дополнений элементов транспонированной матрицы .

Для определения обратной матрицы поступают следующим образом:

1. Пусть дана матрица (2)

2. Составим транспонированную матрицу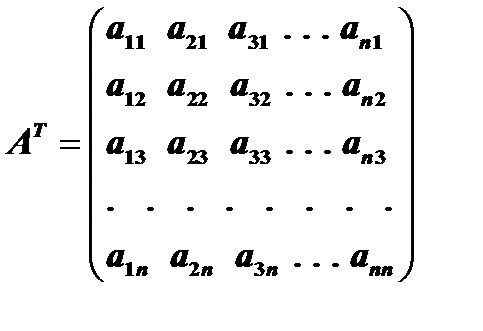

3. Составим присоединенную матрицу

4. Вычислим определитель матрицы (2)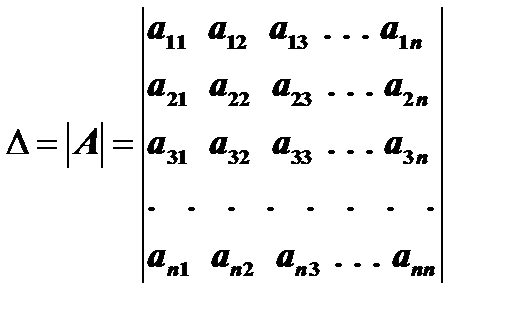

5. Обратная для данной матрицы (2) матрица 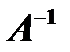получается из присоединенной к 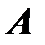матрицы 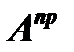путем умножения на число 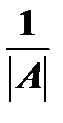, т.е. вычисляется по формуле

.

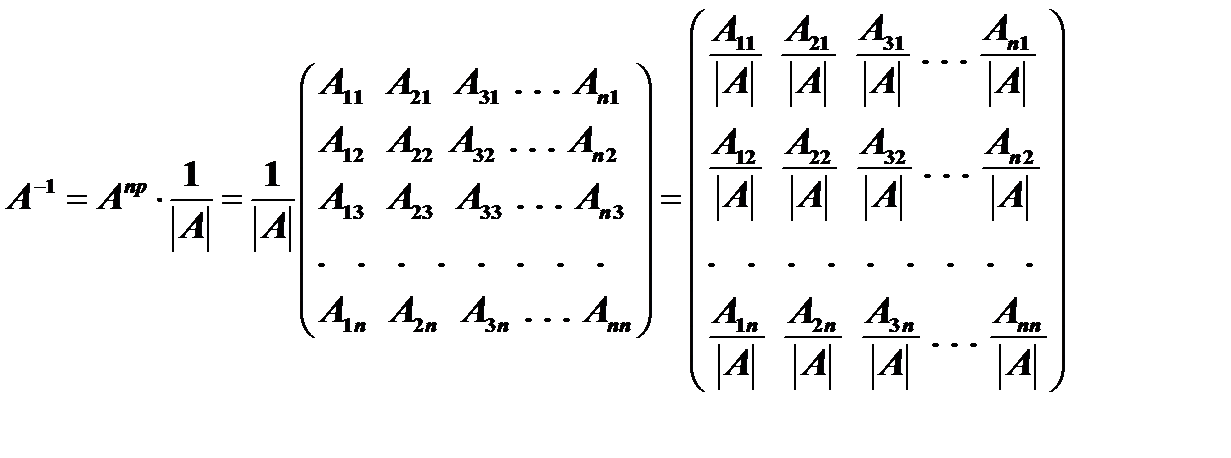Примечание. Обратную матрицу можно вычислить и с помощью элементарных преобразований. Любую квадратную матрицу 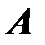путем элементарных преобразований только столбцов (или только строк) можно привести к единичной матрице 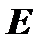. Если совершенные над матрицей 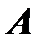элементарные преобразования в том же порядке применить к единичной матрице 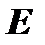, то в результате получится обратная матрица 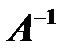. Удобно совершать элементарные преобразования над матрицам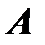и и 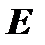одновременно, записывая обе матрицы рядом через черту. При отыскании канонического вида квадратной матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. В случае, когда одновременно надо найти обратную матрицу (если таковая существует), в процессе преобразований следует использовать только строки или только столбцы.