 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Умножение матриц. Произведение матрицы на матрицу определяется в предположении, что число столбцов матрицы равно числу строк матрицы
|
|
Произведение матрицы  на матрицу
на матрицу  определяется в предположении, что число столбцов матрицы
определяется в предположении, что число столбцов матрицы  равно числу строк матрицы
равно числу строк матрицы  .
.
Пусть даны две матрицы  и
и 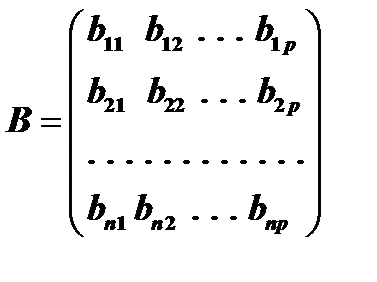 .
.
Произведением двух матриц  и
и 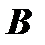 , заданных в определенном порядке (
, заданных в определенном порядке ( - первая и
- первая и 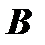 - вторая), называется матрица
- вторая), называется матрица  , элементы
, элементы  которой определяются по следующему правилу: элемент
которой определяются по следующему правилу: элемент  ой строки и
ой строки и  го столбца матрицы
го столбца матрицы  равен сумме произведений элементов
равен сумме произведений элементов  ой строки матрицы
ой строки матрицы  на соответствующие элементы
на соответствующие элементы  го столбца матрицы
го столбца матрицы  , т.е.
, т.е.  .
.


Произведение матриц обладает следующими свойствами:
1) вообще говоря,  , т.е. произведение матриц некоммутативно;
, т.е. произведение матриц некоммутативно;
2) произведение матрицы 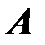 на единичную матрицу
на единичную матрицу  равно самой матрице
равно самой матрице  , т.е.
, т.е.  ;
;
3) произведение матриц подчиняется ассоциативному (сочетательному) закону, т.е.  ;
;
4)  ;
;
5) Для произведения и суммы матриц выполняется дистрибутивный (распределительный) закон  и
и 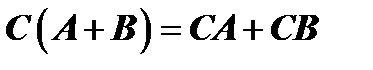 .
.
Дата публикования: 2015-09-17; Прочитано: 327 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
