Изотермы Ван-дер-Ваальса. Критическое состояние вещества

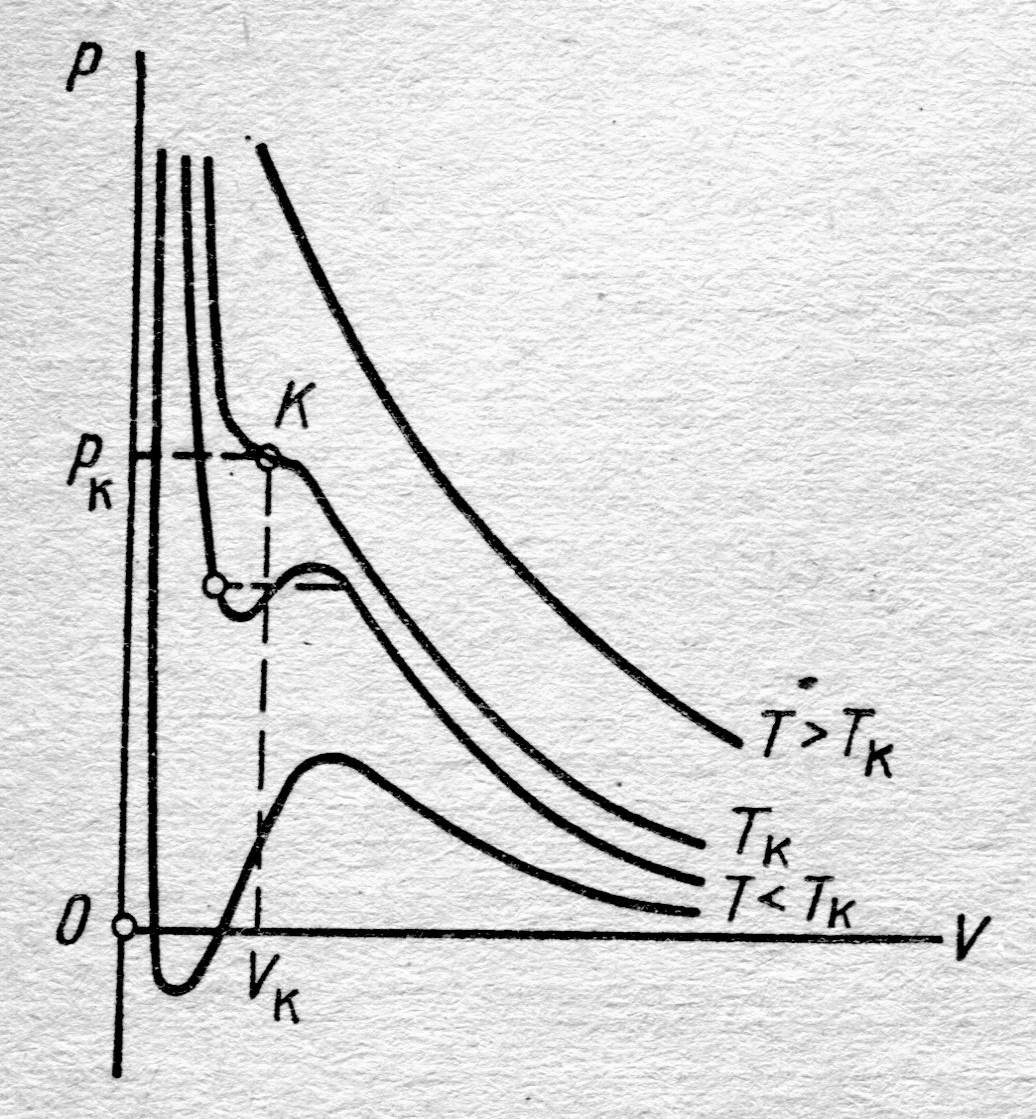
Рис. 8.3. Изотермы Ван-дер-Ваальса

Итак, подход к рассмотрению «столкновений» атомов реального газа как результат наличия сил отталкивания между ними, зависящих от расстояния r и быстро возрастающих при уменьшении r (8.2), позволил получить уравнение Ван-дер-Ваальса (8.8). Оказалось, уравнение Ван-дер-Ваальса есть алгебраическое уравнение третьей степени относительно объёма V. Поэтому, в зависимости от значений давления p и температуры T, может быть одно или три значения объёма V. При постоянной температуре уравнение (8.7) даёт некоторую связь между объёмом и давлением, которая графически представлена на рис. 8.3. Эти кривые принято называть изотермами Ван-дер-Ваальса. При очень высоких температурах, U _эф << k × T, они имеют форму близкую к гиперболе, PV = RT = const, и описывают состояние вещества, близкое к идеальному газу; на такой изотерме каждому значению давления p соответствует одно значение молярного объёма V _о, так же как это имеет место при подчинении газа закону Менделеева-Клапейрона. По мере уменьшения температуры форма изотермы изменяется и при температуре Т _к обнаруживает точку перегиба; рис. 8.3, обозначено символом К. При дальнейшем понижении температуры в определённой области давлений и объёмов, рис. 8.3, изотермы реального газа приближаются к изотермам Ван-дер-Ваальса. В частности, на изотермах проявляются горбы, и каждому давлению p соответствуют три значения объёма V _о.

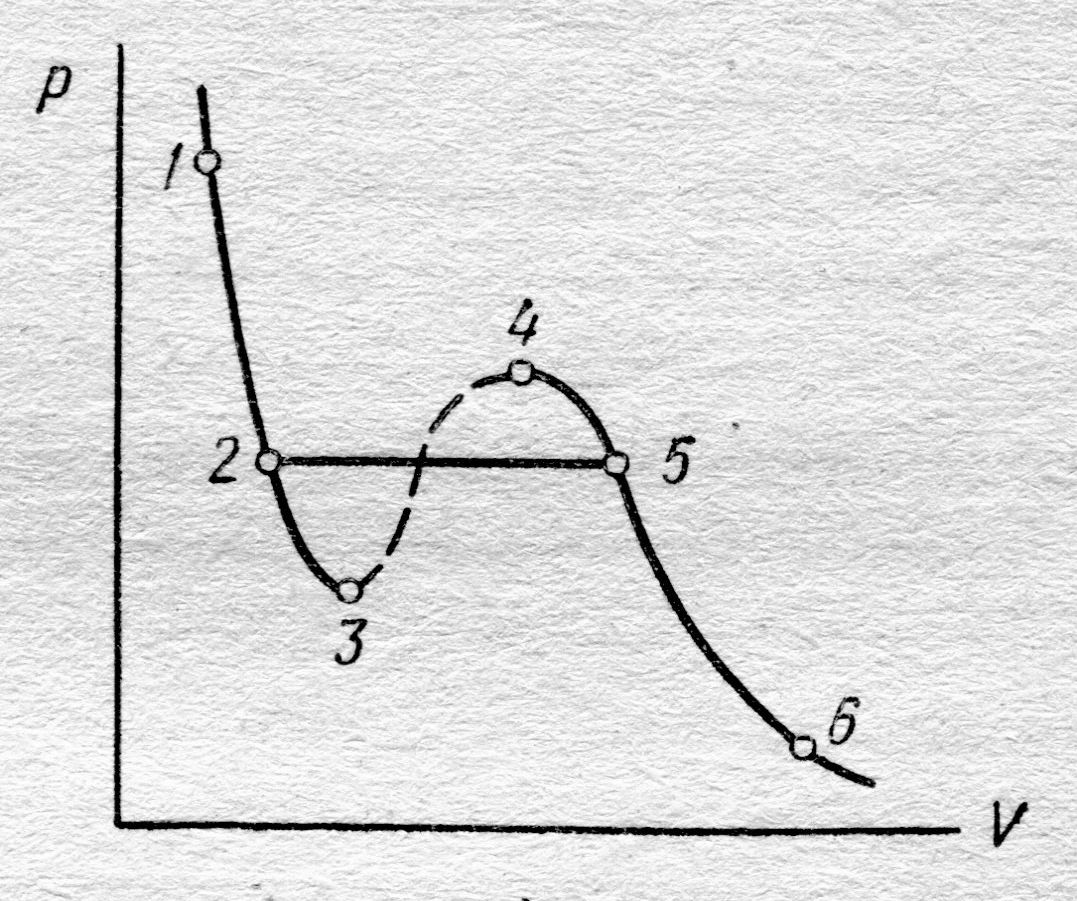
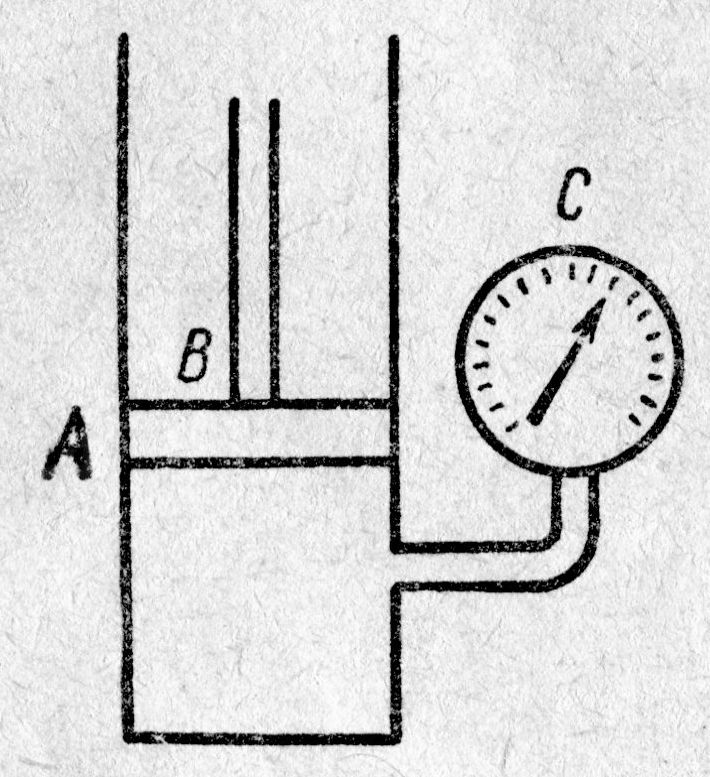
Рис. 8.4. Пояснения в тексте.

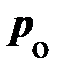
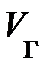
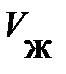Чтобы выяснить смысл этой, странной на первый взгляд, зависимости, обратимся к опыту. Схема опыта следующая (рис. 8.4): в цилиндре А под поршнем В заключён один моль реального газа, температура которого поддерживается постоянной. Объём реального газа V _о может быть измерен по положению поршня В, а его давление – манометром С. На рис. 8.4, сверху, представлена экспериментально полученная изотерма при температуре ниже критической. Измерения показывают, при больших объёмах V _о с опусканием поршня В, объём реального газа уменьшается, а давление возрастает монотонно (рис. 8.4., участок изотермы 6®5); свойства реального газа аналогичны свойствам идеального газа.

При достижении некоторого определённого давления изотерма реального газа идёт не по кривой 5®4®3®2 (рис. 8.4), как этого требует уравнение (8.7), а по изобаре 5®2, т. е. в точке 5 свойства реального газа резко изменяются; происходит расслоение вещества на две фазы: жидкую и газообразную. При дальнейшем опускании поршня давление насыщенного пара p _о, начиная с точки 5, остаётся постоянным; начинается процесс конденсации (ожижения) реального газа. Чем дальше опускается поршень, тем 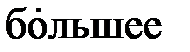количество газа, который при этих условиях принято называть насыщенным паром, конденсируется в жидкость; переход осуществляется при p _о = const (рис. 8.4, 5®2). Точка 2 (рис. 8.4) соответствует переходу всего количества реального газа в жидкую фазу, а ход изотермы примерно следует уравнению (8.7). Под поршнем окажется только жидкость, и дальнейшее продвижение поршня требует весьма значительных усилий.

Таким образом, уравнение Ван-дер-Ваальса описывает не только газообразные состояния вещества, но охватывает и процесс перехода вещества в жидкость, и процесс её сжатия.

В хорошем соответствии с результатами измерений уравнение Ван-дер-Ваальса показывает сближение точек 5®2, соответствующих объёмам V _г и V _ж, по мере повышения температуры (рис. 8.4 и 8.3). Горизонтальный участок изотермы сокращается, стягиваясь в точку К. Температура, соответствующая изотерме с точкой К, а вместе с ней объём и давление (рис. 8.3) принято называть критическими – T _к, P _к, V _к. При T _к исчезает всякое различие между жидкостью и паром. Предпримем усилия по нахождению взаимосвязи между критическими параметрами состояния T _к, P _к, V_ок для одного моля газа и постоянными а и b уравнения Ван-дер-Ваальса.

Преобразуем уравнение Ван-дер-Ваальса:

,

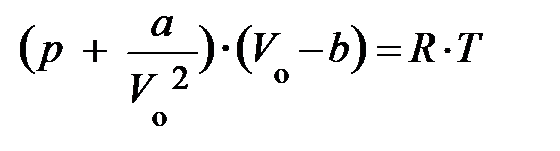раскрыв скобки (выполнили?), умножив левую и правую части на V _о²/ р (сделали?) и собрав члены, содержащие V _о в одинаковых степенях, приходим к выражению вида:

.

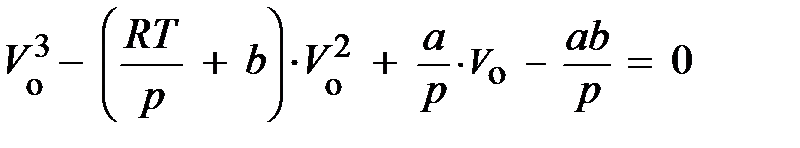Отсюда непосредственно следует, уравнение Ван-дер-Ваальса представляет собою уравнение третьей степени относительно V _о. Запишем его для критической температуры T _к:

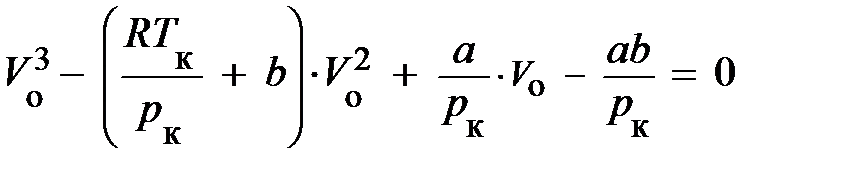. (8.9)

Изотерма с температурой T _к, рис. 8.3, в точке К имеет перегиб, поэтому в этой точке уравнение (8.9) имеет тройной корень V _ок и, как доказывается в алгебре, может быть представлено в виде:

;

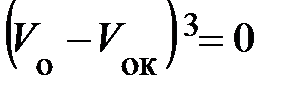если выполнить возведение в степень, то

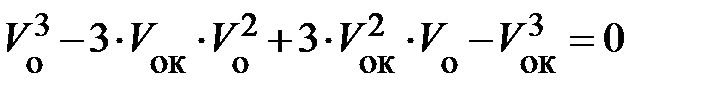. (8.9а)

Оба уравнения (8.9) и (8.9 а) тождественно совпадают между собой, если коэффициенты при одинаковых степенях V _о равны, т. е.:

.

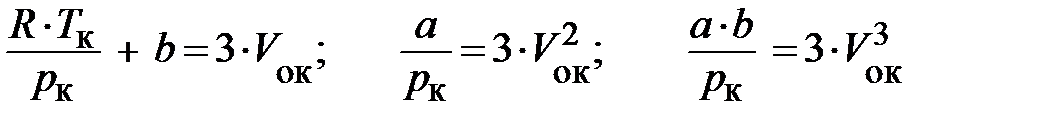Решая эти уравнения относительно трёх неизвестных, пытливый читатель, например, разделив последнее равенство на предпоследнее, получит:

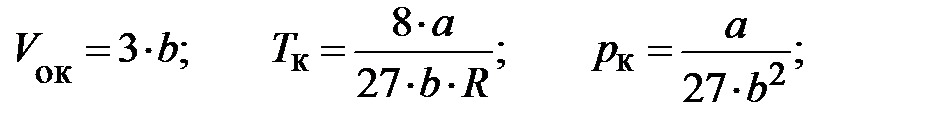
где 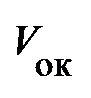– объём одного моля реального газа при критической температуре.

В заключение обратим внимание на то, что экспериментальная изотерма 2®5 (рис.8.4) имеет прямолинейный участок вместо завитка 5®4®3®2. Это объясняется неустойчивостью однородных состояний, отвечающих завитку 5®4®3®2.Если пытливый читатель возьмёт производную на участке 3®4 и, проявив терпение, запишет её через приращение, т. е. D р /D V, то убедится, что она положительна(?). Это означает – увеличение объёма сопровождается ростом давления, что, естественно, является противоестественным.

На участках 2®3 и 3®4 D р /D V отрицательна (убедились?), эти участки могут быть реализованы. Однако в силу их неустойчивости (метастабильны) они требуют выполнения соответствующих условий, в частности, исключения посторонних примесей. Участок 5®4 соответствует пересыщенному пару, а 2®3 – перегретой жидкости. Свойства этих состояний нам потребуются в третьем семестре основного курса физики.