Преобразования Лоренца

Завершая анализ свойств пространства и времени, будем исходить из твёрдо установленных на опыте фундаментальных принципов. Из них, в частности, следует, процедура синхронизации часов в произвольной инерциальной системе отсчёта (ИСО) может осуществляться светом, и при этом с > V, но необязательно с >> V.

Рис. 4.4. Пояснения к преобразованиям Лоренца

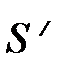
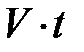
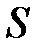
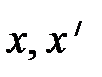
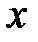
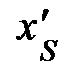
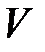
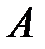
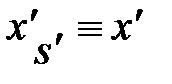Снова обратимся к случаю, когда система S ^/ движется со скоростью V направо вдоль оси Х системы S (рис. 4.4). Координата события в • А 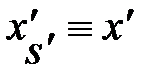– это расстояние, измеренное от точки А до начала отсчёта движущейся ИСО S ^/ (верхняя пунктирная линия). То же расстояние, измеренное по отношению к неподвижной системе отсчёта S, запишется (см. рис. 4.4):

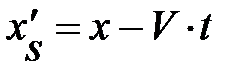. (4.10)

Учитывая взаимосвязь длин отрезков в подвижной и в неподвижной системе отсчёта уравнения (4.8), 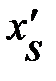может быть записано в виде:

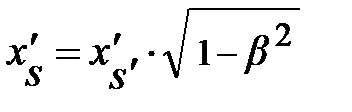. (4.11)

Приняв к сведению, что 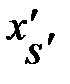тождественно равно 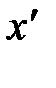, на символическом языке (рис. 4.4), на основе выражений (4.10) и (4.11) немедленно получаем систему уравнений:

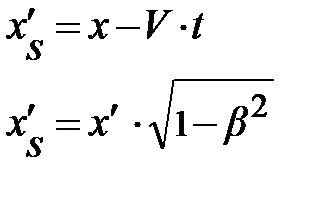
. (4.12)

Поскольку левые части системы уравнений (4.12) равны, после несложных преобразований пытливый читатель получает уравнение, отражающее взаимосвязь координат в движущейся (S ^/) и неподвижной (S) инерциальных систем отсчёта (ИСО):

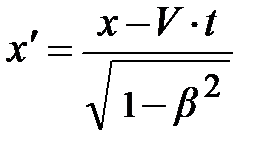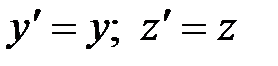; . 4.13)

Убедились? Теперь перейдём к получению взаимосвязи моментов времени произвольного события. Из формулы (4.6) время в движущейся системе отсчёта , умножив числитель и знаменатель на множитель 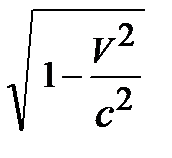, приходим к уравнению вида: 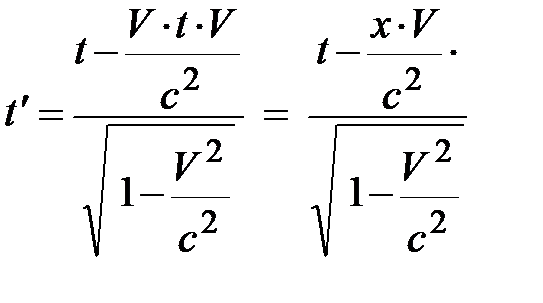. Здесь учтено, V × t – расстояние, пройденное движущейся ИСО S ^/ за время t. Если принять к сведению, что отношение V ²/ с ² может быть заменено постоянной b – бета, приходим к взаимосвязи моментов времени произвольного события и релятивистскому закону сложения скоростей вида:

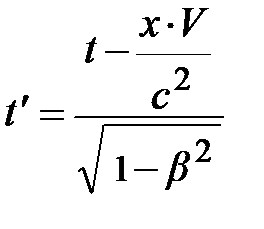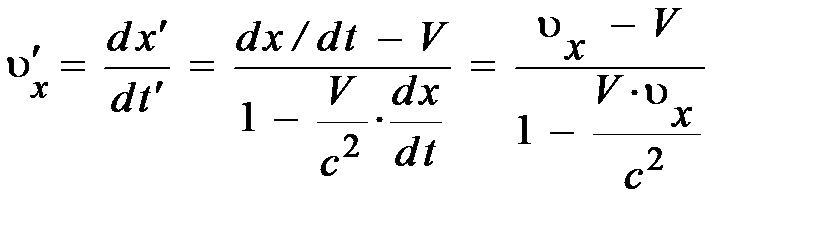. . (4.14)

Такого рода соотношения (4.13) и (4.14) называются преобразованиями Лоренца. Впервые они были выполнены Лоренцем. Он обратил внимание на то, что после таких преобразований форма уравнений Максвелла в теории электромагнетизма не изменяется. Для Эйнштейна этот факт оказался решающим аргументом при формулировке принципа относительности и существования предельной скорости движения материальных объектов.