Закон сохранения момента импульса

Благодаря гибкости понятия частицы нам удалось найти способы описания свободного вращения реальных объектов. Один из приёмов – выбор составных частей системы, для которых мы могли пренебречь внутренним движением и ограничиться рассмотрением только вращательного движения системы (объекта). В частности, при описании свободного движения мы говорили о точке или оси вращения объекта, точнее – оси симметрии, всегда проходящей через его (объекта) центр инерции. При этом угловая скорость w и момент импульса системы Jw направлены строго по оси симметрии. Если ось вращения не совпадает с осью симметрии а. т. т., направление вектора угловой скорости не сохраняется.

Момент инерции а. т. т. J относительно оси симметрии (оси свободного вращения) характеризует его инертные свойства к вращательному движению. Численное значение момента инерции а. т. т определяется не только массами частиц, его образующих, но и их распределением относительно оси симметрии.

Если обратить внимание на уравнение (3.23), то из него, после несложных преобразований, следует:

, (3.24)

т.е. изменение момента импульса тела DL определяется импульсом момента силы M_вр× Dt; DL = M_вр× Dt.

Из последней формулы выражения (3.24) следует, что при отсутствии импульса момента сил, M_вр× Dt = 0, момент импульса остаётся постоянным, то есть DL = L ₂ – L ₁ = 0; откуда немедленно следует L ₂ = L ₁. Это следствие и известно под названием закона сохранения момента импульса. На символическом языке это запишется: D (Jw) = const. На знаковом языке это запишется так: при отсутствии внешних сил и неизменном моменте инерции угловая скорость вращающегося тела остаётся постоянной. Если же при отсутствии внешних сил меняется момент инерции, то начинает меняться и угловая скорость J ₁ w ₁ = J ₂ w ₂. Следует заметить, момент импульса величина векторная и его направление определяется вектором угловой скорости.

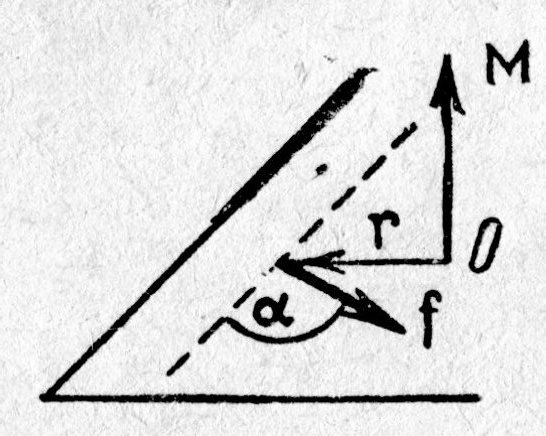
Рис. 3.7. К пояснению понятия момента силы

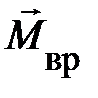Здесь уместно пояснить понятие момента силы , величина которого была представлена векторным произведением 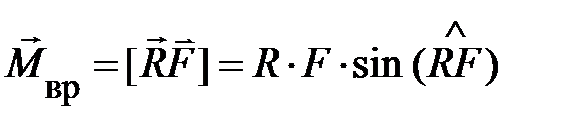. Обратимся к рис. 3.7. Пусть сила f создаёт вращающий момент относительно точки 0. Полную характеристику момента составляют: плоскость, в которой лежат сила f и точка 0; направление, в котором действует сила f; численное значение момента силы, равное произведению силы f на её плечо d, равное r×sina (для понимания аналитической записи плеча мысленно или на бумаге провести на направление силы перпендикуляр из точки 0, а затем учесть, что сумма углов в треугольнике равна 90^о). Все эти три характеристики могут быть выражены одним вектором 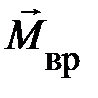, если воспользоваться векторным произведением: 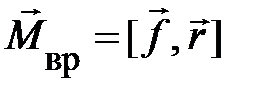. При этом численное значение вектора равно произведению 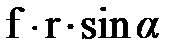. Направление вектора 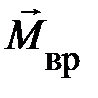выберем так, чтобы он был перпендикулярен плоскости, содержащей векторы 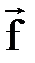и 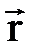, и в таком направлении, чтобы при рассмотрении с его конца вектор 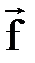мог быть совмещён с вектором 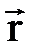путём вращения в направлении уменьшения угла между ними. Всё это совпадает с представлением о векторном произведении, а псевдовектор момент силы определяет, исходя из выражения (3.23), направление углового ускорения e.

Если у въедливого читателя появилось желание проверить справедливость закона сохранения момента инерции при свободном вращении, есть предложение. Преобразуйте последнее равенство выражения (3.24) к виду: 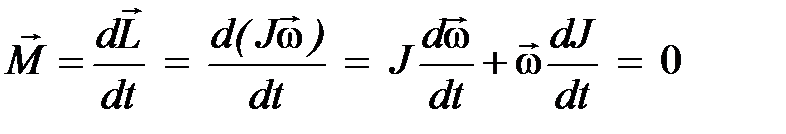. Опять же, из последнего равенства выразите 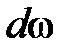. Сделали?

А теперь, если есть возможность, встаньте на диск здоровья. Попросите, чтобы вас раскрутили. Разведите руки в стороны. Прочувствовав изменения в вашем свободном вращении, отметьте на бумаге, в каком случае угловая скорость была больше. Запишите это на носителе, бумажном. Можно подставлять полученный результат в формулу для 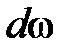. Удачи в поиске истины. Вопросы приветствуются.