Пространственно-временной интервал как объективная характеристика мира событий

Из преобразований Лоренца (4.13) и (4.14) следует, расстояние D r и промежуток времени D t сами по себе не пригодны для объективного описания пространственно-временных отношений между событиями в совокупности произвольно движущихся ИСО. Задача состоит в том, чтобы найти комбинацию из неинвариантных по отдельности величин D r и D t, которая не изменялась бы относительно всех ИСО.

Решая её, следует исходить лишь из твёрдо установленного факта неизменности скорости света в любых двух ИСО. А именно, рассмотрим относительно систем S и S ^/ два специфических события – испускание светового сигнала и последующий его приём. Из равенства с ^/ = с следует, что для таких событий с ^/ = D r ^/ /D t ^/ = D r /D t = с. Это значит, что определённая комбинация из расстояния D r и промежутка времени D t

с ²×(D t ^/)² – (D r ^/)² = с ²×(D t)² – (D r)² = 0

остаётся здесь неизменной, хотя сами по себе расстояние (D r ¹ D r ^/) и промежуток времени (D t ¹ D t ^/) могут изменяться.

Переходя к рассмотрению пары произвольных событий, введём для них, по аналогии с приведённым примером, новую величину D I, называемую пространственно-временным интервалом между событиями или просто интервалом. По определению квадрат интервала запишется:

D I ² = с ²×D t ² – D r ² = с ²×D t ² – D x ² – D y ² – D z ². (4.15)

Если в предыдущем примере он был равен нулю, то для произвольных событий он отличен от нуля. Однако, согласно преобразованиям Лоренца (4.13), (4.14) остаётся инвариантом, неизменным в любой ИСО:

D I ^/ º D I. (4.16)

Убедимся в этом. В системе S ^/

D t ^/ = g× 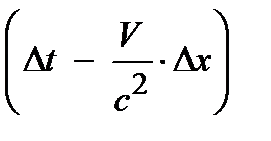; D x ^/ = g×(D x – V ×D t); D y ^/ = D y; D z ^/ = D z; здесь g = 1/ .

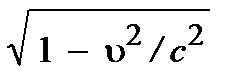Тогда, с учётом (4.13) D I ^{/ 2} = с ²×D t ^{/ 2} – D x ^{/ 2} – D y ^{/ 2} – Dz ^{/ 2} =

= c ²×g²× – g²×(D x – V ×D t)² – D y ² – D z ² =

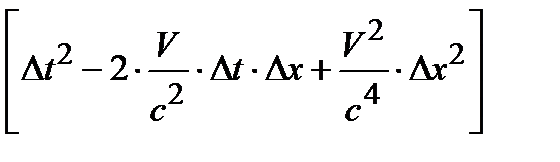= c ²×g²× – g²× 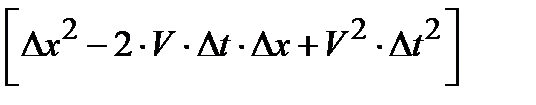– D y ² – D z ².

В последнем равенстве после раскрытия квадратных скобок слагаемые, с удвоенным произведением, сокращаются. Объединив члены с D t ² и D x ², получаем

D I ^{/ 2} = D t ²×g²×(с² – V ²) – D x ²×g²×(1 – V ²/с²) – D y ² – D z ² = с ²×D t ² – D x ² – D y ² – D z ² = D I ²,

Здесь пытливый читатель должен увидеть, что произведение скобок с g² ведёт к 1.

Проведённые преобразования позволяют утверждать, что именно интервал D I, а не расстояние D r и промежуток времени D t по отдельности следует считать объективной характеристикой пространственно-временных отношений. Таким образом, «переворот, произведённый Эйнштейном во взглядах на пространство и время, вовсе не сводится к установлению взаимосвязей пространственных и временных отношений или относительности некоторых понятий. Заслуга Эйнштейна, скорее, в том, что вместо одних «очевидно» инвариантных величин (D r и D t) он ввёл другие инвариантные величины (D I), более пригодные для отражения объективных свойств мира событий, установления подлинного единства пространственных и временных отношений» [2].

Убедимся в том, что понятие интервала D I богаче понятия расстояния. Расстояния в пространстве либо всегда положительны, либо равны нулю: D r ³ 0. В то же время в мире событий кроме DI ² < 0 – пространственноподобных интервалов, могут существовать интервалы с DI ² > 0, называемые времениподобными и с DI ² = 0 – светоподобными. Для пар событий, разделённых времениподобными интервалами с DI ² > 0, вместо интервала DI можно ввести более удобное понятие – собственное время движущегося объекта. Действительно, пусть в системе S с постоянной скоростью u движется частица с массой m ¹ 0. За промежуток времени D t она сместится на расстояние D r = u ×D t. Интервал DI между событиями, соответствующий началу и концу её движения, в системе S равен:

DI =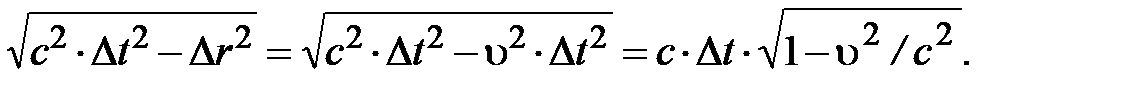

Перейдём в ССО (собственную или сопровождающую систему отсчёта) S ^/ = S _о, движущуюся относительно S с той же скоростью 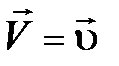, что и сама частица. В ней скорость частицы 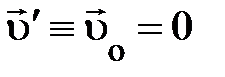, так что пространственно-временной интервал , где 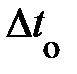– промежуток времени между событиями по часам в ССО. Из инвариантности интервала 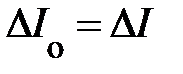следует инвариантность промежутка времени:

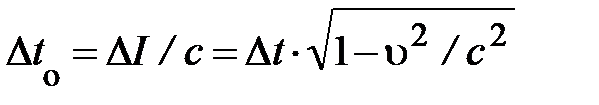. (4.17)

Величину 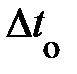принято называть собственным временем частицы (и связанной с нею ССО).

В заключение параграфа заметим, несмотря на то, что хотя промежуток времени D t между парой одних и тех же удалённых событий с D I ² > 0 относителен, понятия «раньше», «позже», «одновременно» для этой пары событий абсолютны. Они все, согласно (4.17), определяются инвариантной величиной 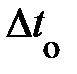. Иными словами, если 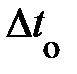> 0, то из двух событий второе происходит позже (D t > 0), если 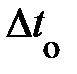< 0, то оно происходит раньше (D t < 0), и, наконец, если 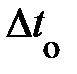= 0, то оба события одновременны (D t = 0) во всех ИСО. Иначе говоря, для времениподобных интервалов знак времени не зависит от выбора ИСО.