Перпендикулярность прямой линии и кривой поверхности

Утверждение 16.6. Если прямая линия р перпендикулярна к плоскости

Рис. 16.89. Графическая модель прямой а и плоскости a, перпендикулярных к эллипсоиду вращения Ф

a в обыкновенной точке А её касания

к кривой поверхности Ф, то она пер-пендикулярна к этой поверхности.

а ^[(a Ç Ф) ' А Î Ф ] Þ а ^ Ф.

Задача 16.27. Построить двухкар-тинный комплексный чертёж прямой p, перпендикулярной к сфере Ф в её обыкно-венной точке А (рис. 16. 88).

Решение: 1. Через точку А на сфере Ф провести горизонтальную параллель b (b₂, b₁) и фронтальную параллель с (с₁, с₂);

2. Через точку А провести плоскость a (f ´ h), касательную к поверхности Ф. При этом f₁ ^ A₁ A₂, f₂ ^ o₂ A₂; h₂ ^ A₁A₂, h₁ ^ o₁A_1.

3. Из точки А восставить перпендику-ляр р к плоскости a: (р₁ ^ h₁, p₂ ^ f₂), кото-рый является искомым перпендикуляром к поверхности Ф и её нормалью в точке А.

Утверждение 16.7. Многообразием нормалей к сферической поверхности яв-ляется связка радиусов всех окружностей

большого круга, проходящих через все её точки.

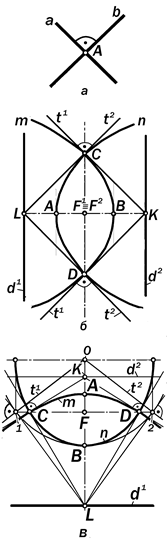
Рис. 16.90. Ортогонально-сопраженные линии:

а – прямые t¹ и t²;

б – софокусные параболы

в – софокусные гипербола и эллипс

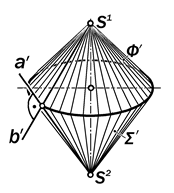
Рис.16.91. Геометрическая модель ортогонально-сопряженных конических поверхностей Ф и S

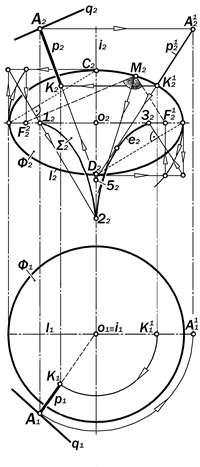
Пример 16.29. Построить двухкартин-ный комплексный чертёж прямой р, пер-пендикулярной к поверхности эллипсоида вращения Ф и проходящей через произво-льную точку А пространства (рис.16.89 )

Решение: 1. Вращением вокруг і по-вернуть точку А до совпадения с плоскоc-

тью главного меридиана l эллипсоида Ф. Для этого: і₁А₁ Ç (і₁А₁¹ ^ А₁А₂);

А₂ ® (А¹ ^ А₁ А₂).

2. Взять на очерке фронтальной прое-кции l₂ эллипсоида Ф несколько точек и соединив их с его фокусами, провести бис-сектрисы образовавшихся углов как соот-ветствующих нормалей к эллипсу l₂ в этих точках (на рис.16.89 условно не показаны);

3. Обогнуть продолжения проведенных нормалей и получить тем самым эволюту е₂ эллипса l₂ как очерк фронтальной проек-ции S₂ фокальной поверхности S эллипсо-ида Ф;

4. Из точки А₂¹ провести проекцию р₂¹ прямой р, касательно к е₂ и отметить точки 5₂ её пересечения с i₂ и К₂¹ – с l₂, а А₁ соединить с о₁ º i_1;

5. Соединить А₂ с 5₂ и определить на А₂5₂ положение К₂ – проекции основания перпендикуляра р к поверхности Ф;

6. По К₂ на А₁ о₁ определить К₁ как го-ризонтальную проекцию основания норма-ли р ^ Ф.

7. Плоскость a (p x q) ^ Ф.

Определение 16.6. Поверхность S, образованная вращением эволюты е элли-пса l эллипсоида Ф вокруг оси его враще-ния называется фокальной поверхностью этого эллипсоида.

Утверждение 16.8 Многообразием ка-сательных к фокальной поверхности S данной поверхности вращения Ф являет-

ся конгруэнция нормалей поверхности Ф.

Правило 1. Для того, чтобы постро-ить комплексный чертёж конгруэнции нормалей к поверхности вращения, необ-ходимо построить проекции её фокальной поверхности, а затем изобразить необхо-димое и достаточное количество прямых, которые касательны к ней.