Сопряжения конических поверхностей плоскостями

(рис.16.76 – 16.78))

Для графического моделирования двух конических поверхностей Ф и S, одинаковой конусности, вершины кото-рых расположены по одну сторону от их оснований, сопряженных двумя пло-скостями a и b, следует прежде изо-бразить внешнее сопряжение двух ок-ружностей прямыми линиями, затем принять эти окружности за основания

Рис. 16.76. Графическая модель двух конических поверхностей Ф и S, сопряженных двумя плоскостями внешним образом

сопрягаемых поверхностей, прямые, касательные к ним, - за горизонтальные следы касательных плоскостей a и b, а

Рис.16.77. Геометрическая модель конических поверхностей Ф и S, сопряженных двумя плоскостями внутренним образом

точки их касания к окружностям – за на-чала тех пар параллельных образую-

щих данных поверхностей, по которым

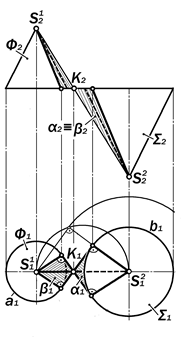
Рис. 16.78. Графическая модель конических поверхностей Ф и S, сопряженных плоскостями a и b внутренним образом

Рис.16.79. Графическая модель двух конических поверхностей Ф и S, сопряженных конической поверхностью D внутренним образом

плоскости a и b их касаются.

Будучи непараллельными между собой, плоскости a и b пересекаются по прямой линии е, соединяющей вер-шины поверхностей Ф и S.

Если две конические поверхности Ф и S одинаковой конусности сопря-гаются двумя плоскостями a и b внут-ренним образом (рис. 16.77), то их вер-шины должны располагаться по разные стороны от плоскости их оснований, а прямые, касательные к основаниям,

должны проходить через точку К пере-сечения прямой е, соединяющей вер-шины поверхностей, с плоскоcтью их оснований.

Для графического моделирования двух конических поверхностей Ф и S, разной высоты, но одинаковой конусно-сти, сопряженных плоскостями a и b внутренним образом (рис.16.78) следу-ет прежде изобразить план двух го-ризонтальных окружностей разного ди-аметра, сопряженных внутренним обра-зом двумя пересекающимися прямыми.

После этого следует принять окружно-сти за основания конических поверхно-стей Ф и S, вершины которых распо-лагаются по разные стороны от плос-кости их основания, сопрягающие их прямые - за следы искомых сопрягаю-щих плоскостей a и b, а точки касания

1, 2, 3, 4 – за начала линий их касания к поверхностям Ф и S и изобразить их фронтальную проекцию.

Сопряжения конических поверхностей коническими поверхностями (рис.16.79 - 16.81)

Если замкнутую коробовую кривую, состоящую из сопрягающих друг друга дуг окружностей принять за основание

а некоторой поверхности W, то ею явит-ся поверхность, состоящая из двух пар сопряжённых и равнонаклонённых к их

Рис..16.80. Геометрическая модель четырёх сопряженных конических поверхностей на основе четырёхцентрового овала

Рис.16.81. Графическая модель четырёх сопряженных конических поверхностей на основе четырёхцентрового овала

Рис.16.82. Геометрическая модель

торсовой поверхности одинакового

ската

Рис.16.83. Геометрическая модель золотого эллиптического торса

основаниям конгруэнтных конических поверхностей Ф¹, Ф² и S ¹, S², проекция-ми вершин которых являются центры сопряжения образующих это основание дуг.

Как и коническая, поверхность W имеет две полы. Нижняя образована полными фрагментами поверхностей Ф¹ и Ф², сопряженными с неполными фрагментами поверхностей S¹ и S², ко-торые пересекаются по гиперболичес-кому гребню m, сопрягающему в вер-шинах S¹ и S² очерковые образующие фронтальной проекции поверхностей Ф¹ и Ф². Верхняя пола образована пе-ресекающимися по гиперболическому гребню n верхними полами фрагмен-тов поверхностей Ф¹ и Ф². При этом фигура основания верхней полы, ле-жащей в горизонтальной плоскости ве-ршин поверхностей S¹ и S², конгруэн-тна фигуре нижней полы, но развёрну-та по отношению к ней на 90°.

Между верхней и нижней полами существует переходная поверхность Q как некий тетраэдр с коническими гра-нями, двумя гиперболическими и четы-рьмя прямолинейными рёбрами. Вер-шинами этого тетраэдра являются вер-шины сопрягающихся конических пове-

рхностей Ф¹, Ф² и S¹, S. ²

Если вершина S подвижной кони-ческой поверхности перемещается по пространственной линии m, то возника-ет огибающая её положения торсовая поверхность одинакового ската (рис.82)