 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Група геометричних перетворень та її підгрупи
|
|
Розглянемо множину  елементів довільної природи та вважатимемо, що на ній задана бінарна операція, тобто правило, за яким кожним двом елементам цієї множини поставлено у відповідність єдиний елемент цієї ж множини. Позначимо дану операцію символом
елементів довільної природи та вважатимемо, що на ній задана бінарна операція, тобто правило, за яким кожним двом елементам цієї множини поставлено у відповідність єдиний елемент цієї ж множини. Позначимо дану операцію символом 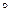 .
.
Пару  називають групою, якщо:
називають групою, якщо:
1) бінарна операція 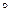 асоціативна, тобто для довільних елементів
асоціативна, тобто для довільних елементів  виконується рівність
виконується рівність  ,
,
2) існує елемент  такий, що для довільного
такий, що для довільного  виконується умова
виконується умова  (елемент
(елемент  у цьому випадку називають нейтральним),
у цьому випадку називають нейтральним),
3) для довільного  у множині
у множині  знайдеться елемент
знайдеться елемент  такий, що
такий, що  (елемент
(елемент  називають симетричним до
називають симетричним до 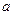 та позначають
та позначають  ).
).
Нехай  - деяка підмножина множини
- деяка підмножина множини  та
та  є групою. Тоді її називають підгрупою групи
є групою. Тоді її називають підгрупою групи  .
.
Теорема. Для того, щоб група  була підгрупою групи
була підгрупою групи  необхідно та достатньо, щоб виконувалися такі умови: 1) для довільних елементів
необхідно та достатньо, щоб виконувалися такі умови: 1) для довільних елементів  елемент
елемент  належить підмножині
належить підмножині  , 2) для довільного елемента
, 2) для довільного елемента 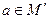 симетричний до нього елемент
симетричний до нього елемент  теж належить множині
теж належить множині  .
.
Дальше ми побачимо важливість понять групи та підгрупи в геометрії, але спочатку зупинимось на деяких нових означеннях, які стосуються теорії геометричних перетворень.
Оскільки перетворення площини є взаємно однозначним відображенням, то поряд із кожним перетворенням 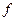 , яке різним точкам площини ставить у відповідність їх різні образи, можна розглядати інше відображення, яке кожному образу ставить у відповідність його прообраз. Очевидно, що це відображення теж є перетворенням площини.
, яке різним точкам площини ставить у відповідність їх різні образи, можна розглядати інше відображення, яке кожному образу ставить у відповідність його прообраз. Очевидно, що це відображення теж є перетворенням площини.
Таке перетворення називають оберненим до 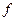 та позначають
та позначають 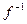 . Таким чином, якщо
. Таким чином, якщо  , то
, то  . Відмітимо, що серед наведених вище прикладів оберненим до паралельного перенесення на вектор
. Відмітимо, що серед наведених вище прикладів оберненим до паралельного перенесення на вектор 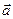 є паралельне перенесення на вектор -
є паралельне перенесення на вектор - 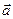 , тобто
, тобто  , а перетворенням, оберненим до повороту навколо точки
, а перетворенням, оберненим до повороту навколо точки 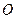 на кут
на кут 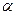 є поворот навколо даної точки на кут -
є поворот навколо даної точки на кут - 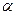 :
: 
 . Нескладно переконатися також у тому, що
. Нескладно переконатися також у тому, що 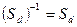 ,
,  .
.
Розглянемо множину  всіх перетворень площини та візьмемо з неї два довільні перетворення
всіх перетворень площини та візьмемо з неї два довільні перетворення 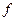 та
та 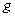 . Нехай при перетворенні
. Нехай при перетворенні 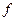 точка
точка  відображається у точку
відображається у точку  , а при перетворенні
, а при перетворенні 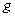 точка
точка  переходить у точку
переходить у точку 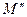 . Відображення, при якому точці
. Відображення, при якому точці  ставиться у відповідність точка
ставиться у відповідність точка 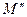 теж є перетворення площини, оскільки при кожному із виконаних перетвореннях
теж є перетворення площини, оскільки при кожному із виконаних перетвореннях 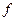 та
та 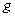 різні точки переходять у різні.
різні точки переходять у різні.
Одержане перетворення, яке ми позначимо через  , називають композицією перетворень
, називають композицією перетворень 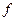 та
та 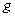 і записують у виді
і записують у виді 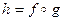 . Отже, згідно із введеним означенням,
. Отже, згідно із введеним означенням,
 .
.
Покажемо, що пара  , тобто множина всіх перетворень площини
, тобто множина всіх перетворень площини  із введеною на ній бінарною операцією
із введеною на ній бінарною операцією 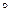 (композицією перетворень), утворює групу. Для доведення зауважимо, що для трьох довільних перетворень
(композицією перетворень), утворює групу. Для доведення зауважимо, що для трьох довільних перетворень  виконується рівність
виконується рівність
 . (1)
. (1)
Справді, згідно з означенням композиції перетворень
 .
.
Аналогічно
 ,
,
що завершує доведення рівності (1).
У ролі нейтрального елемента виступає тотожне перетворення  , оскільки очевидно, що для довільного перетворення
, оскільки очевидно, що для довільного перетворення  виконується рівність
виконується рівність  . На завершення доведення зауважимо, що, як було відмічено вище, для довільного перетворення
. На завершення доведення зауважимо, що, як було відмічено вище, для довільного перетворення  існує обернене перетворення
існує обернене перетворення 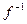 , яке у множині
, яке у множині  виконує роль оберненого (симетричного) елемента, оскільки
виконує роль оберненого (симетричного) елемента, оскільки  .
.
Групу  називають групою геометричнихперетворень.
називають групою геометричнихперетворень.
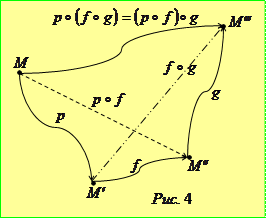 Зауваження. Покажемо дещо інше за формою запису, але по суті аналогічне до розглянутого вище доведення рівності (1). Нехай
Зауваження. Покажемо дещо інше за формою запису, але по суті аналогічне до розглянутого вище доведення рівності (1). Нехай  ,
,  ,
,  (рис. 4).
(рис. 4).
Тоді 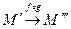 ,
,  , тому
, тому  і
і  , що потрібно було довести.
, що потрібно було довести.
Наведемо приклади підгруп групи геометричних перетворень.
1). Розглянемо множину всіх паралельних перенесень. Нехай при перетворенні  точка
точка  переходить в точку
переходить в точку  , а при перетворенні
, а при перетворенні  точка
точка  переходить в точку
переходить в точку 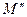 , тобто
, тобто 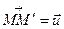 ,
,  . Тоді, оскільки
. Тоді, оскільки 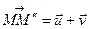 , то
, то  , тобто композиція двох розглянутих паралельних перенесень є паралельне перенесення. Як було сказано вище, оберненим до паралельного перенесення на вектор
, тобто композиція двох розглянутих паралельних перенесень є паралельне перенесення. Як було сказано вище, оберненим до паралельного перенесення на вектор 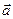 є паралельне перенесення на вектор -
є паралельне перенесення на вектор - 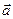 , тобто
, тобто  . Тому множина всіх паралельних перенесень утворює підгрупу групи геометричних перетворень.
. Тому множина всіх паралельних перенесень утворює підгрупу групи геометричних перетворень.
2). Розглянемо множину всіх поворотів навколо фіксованої точки 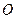 . Нехай при повороті
. Нехай при повороті 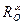 точка
точка  переходить в точку
переходить в точку  , а при повороті
, а при повороті  точка
точка  переходить в точку
переходить в точку 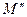 . Тоді, оскільки
. Тоді, оскільки  і
і  , то
, то
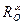
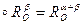 , тобто композиція двох поворотів із спільним центром є поворот навколо даного центра. Перетворенням, оберненим до повороту навколо точки
, тобто композиція двох поворотів із спільним центром є поворот навколо даного центра. Перетворенням, оберненим до повороту навколо точки 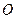 на кут
на кут 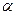 є поворот навколо даної точки на кут -
є поворот навколо даної точки на кут - 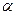 :
: 
 . Отже, множина всіх поворотів навколо фіксованого центра теж утворює підгрупу групи геометричних перетворень.
. Отже, множина всіх поворотів навколо фіксованого центра теж утворює підгрупу групи геометричних перетворень.
Дата публикования: 2015-09-17; Прочитано: 986 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
