Класифікація ліній другого порядку

Розглянемо питання, скільки та які види ліній може задавати рівняння (1). Насамперед нагадаємо, що рівняння (ми уже зустрічали його при дослідженні питання існування головних напрямків (див. лекції 19-20, п. 4)) завжди має корені, причому кут повороту , при якому вісь координатної системи набуває головного напрямку, визначається рівністю (тут - один із коренів характеристичного рівняння).

Обчислимо для рівняння (1) інваріанти 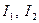, 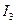та розглянемо спочатку випадок 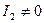, тобто випадок, коли лінія центральна.

Після перенесення початку координат у центр лінії та повороту на кут, при якому координатні осі набувають головних напрямків, рівняння лінії зведеться до виду

. (11)

Складаючи та розв’язуючи характеристичне рівняння 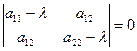або , дістаємо

.

Обчислимо для рівняння (11) інваріант :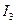

.

Отже, 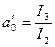. Рівняння (11), таким чином, набуде виду

. (12)

Можливі наступні випадки:

1) 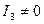, - одного знаку. Немає жодної пари дійсних чисел, які задовольняють рівняння (12). Лінію називають уявним еліпсом. Прикладом уявного еліпса може бути лінія, задана рівнянням .

2) 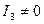, - одного знаку (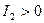), частка - протилежного. Рівняння (12) запишемо у виді . Очевидно, що одержане рівняння задає еліпс.

3) 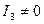, - протилежного знаку (тобто ). Рівняння (12) запишемо у виді . Оскільки знаменники дробів мають протилежні знаки, то одержане рівняння задає гіперболу.

4) 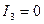, - одного знаку (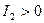). Рівняння має єдиний нульовий розв’язок. В полі комплексних чисел дане рівняння можна записати у виді

,

де . Кажуть, що у цьому випадку лінія вироджується в пару уявних прямих, які перетинаються у дійсній точці. Відповідним прикладом може бути лінія, задана рівнянням з єдиним дійсним розв’язком .

5) 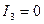, - протилежного знаку (). У цьому випадку рівняння можна записати у виді . Лінія являє собою пару прямих, які перетинаються. Рівняння ілюструє цей випадок. Записавши його у виді , бачимо, що воно задає дві прямі, що перетинаються: та .

Тепер розглянемо випадок, коли 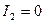, тобто, коли лінія нецентральна. Одним із коренів характеристичного рівняння є число . Після повороту на кут , при якому вісь набуде головного напрямку, рівняння лінії зведеться до виду

, (13)

де - другий корінь характеристичного рівняння. У цьому випадку інваріант

.

Оскільки 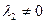, то при 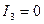дістаємо і рівняння (13) перетвориться у квадратне відносно змінної 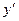. У залежності від дискримінанта дістаємо три випадки:

6) , квадратне рівняння має два різні дійсні корені, а рівняння лінії задає дві паралельні прямі;

7) , квадратне рівняння має два рівні корені, а рівняння лінії задає дві прямі; які співпадають;

8) , квадратне рівняння має два різні уявні корені, а рівняння лінії задає дві уявні паралельні прямі.

Нехай для рівняння (13) 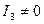, тобто . Виконаємо паралельне перенесення системи координат у новий початок – точку, координати якої знайдемо, розв’язавши систему рівнянь

.

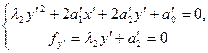Тоді у перетвореному рівнянні коефіцієнти та перетворяться в нуль. Справді, новий початок вибрано на лінії, тому . Оскільки , то .

Обчисливши тепер із умови 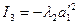невідомий коефіцієнт , дістаємо рівняння лінії у вигляді

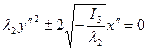. (14)

Одержане рівняння визначає параболу. Зауважимо, що новий початок, в який ми переносили систему координат, є вершиною параболи. Таким чином:

9) якщо 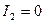та 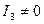, то рівняння (1) визначає параболу.

Підсумовуючи сказане, зробимо наступний висновок. Існує 9 різних типів ліній другого порядку:

1) еліпс, 2) уявний еліпс,

3) гіпербола, 4) парабола,

5) дві прямі, що перетинаються,

6) дві паралельні прямі,

7) дві прямі; що співпадають,

8) пара уявних прямих, що перетинаються у дійсній точці,

9) дві уявні паралельні прямі.