Комплексные числа

В поле действительных чисел неразрешимо простейшее уравнение

x² + 1 = 0.

Для устранения этой проблемы вводится новое число i (мнимая единица) такое, что i² = –1.

Определение. Полем комплéксных чисел называется минимальное поле, содержащее в качестве подполя поле действительных чисел, и в котором содержится элемент, квадрат которого равен – 1. Это поле обозначают буквой С

Символ вида z = a + bi, где a и b – действительные числа, а i – мнимая единица, называется комплексным числом с действительной частью a = Rez и мнимой частью b = Imz. Сложение и умножение в множестве C комплексных чисел осуществляется по правилам:

(a + bi) + (c + di) = (a + c) + (b + d) i,

(a + bi)(c + di) = (ac – bd) + (ad + bc) i.

Не сложно проверить, что все аксиомы поля для множества таких чисел с введёнными операциями выполняются. В частности обратный элемент для любого отличного от 0 числа может быть найден следующим образом:

(a + bi)^-1 = = .

Корректность данного способа проверяется умножением числа на обратное к нему. Действительное число a можно трактовать как комплексное число a + 0 i, так что поле действительных чисел является подмножеством множества C.

Числами вида a + bi исчерпывается все поле комплексных чисел. Поскольку поле является устойчивым относительно сложения и умножения, то вместе с любыми двумя действительными числами a и b, а также мнимой единицей i, оно должно содержать и любое выражение вида z = а + bi, так что построенное поле удовлетворяет условию минимальности. Данная форма комплексного числа называется алгебраической. а называется действительной частью числа, а b – мнимой частью числа.

Идея геометрического представления комплексных чисел заключается в том, что комплексному числу х + yi сопоставляется точка плоскости с координатами (x, y). Данную модель впервые предложил К. Вессель (1799). Другой вариацией является представление комплексного числа матрицей:

.

Каждое комплексное число можно представить в алгебраической и тригонометрической форме z = x + iy = r (cos j + i sin j). Если каждому такому числу z сопоставить матрицу = , то сумме, разности и произведению двух любых комплексных чисел будет соответствовать сумма, разность и произведение соответствующих матриц. Например, произведению чисел (x ₁ + iy ₁) (x ₂ + iy ₂) = (x ₁ x ₂ – y ₁ y ₂) + i(x ₁ y ₂ + x ₂ y ₁) будет соответствовать матрица

= .

Более того, обратное для комплексного числа (x + iy)^–1 = соответствует матрице , которая является обратной к матрице .

Таким образом, деление комплексных чисел также сводимо к умножению матрицы делимого на матрицу обратную к матрице делителя. Поэтому данное множество матриц вида можно считать моделью поля комплексных чисел. Тригонометрическое представление матричной модели интересно ещё и тем, что матрица задает оператор поворота на угол j, что соответствует геометрическому смыслу умножения на комплексное число (при умножении происходит растяжение в r раз и поворот на угол, равный аргументу j).

Можно было ожидать, что при анализе уравнений более высоких степеней возникнет необходимость в дальнейшем обобщении понятия числа. Но в 1799 году К. Гаусс доказал так называемую Основную теорему алгебры.

Теорема. Всякое алгебраическое уравнение степени n с действительными или комплексными коэффициентами a₀xⁿ + a₁x ^n-1 +... + a _n-1 x + a_n = 0 в поле комплексных чисел имеет n корней (с учетом их кратностей).

Однако, получая возможность находить корни всех многочленов, мы теряем возможность сравнивать числа между собой.

Теорема. Поле комплексных чисел не является упорядоченным полем.

Доказательство: Действительно, любое упорядоченное поле должно являться расположенным кольцом, а значит для него справедливо свойство о том, что квадрат любого числа неотрицателен. В поле же комплексных чисел данное свойство не выполняется, так как i ² = –1 < 0.

Задания для самостоятельного решения

№3.4.. Вычислите:

a) (7 – 3 i)³; б) ; в) ; г) i⁵; д) i²²⁸; е) i¹³⁷;

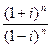ж) (2 + i)²; з) ; и) ; к) .

№ 3.5. Запишите числа комплексно-сопряжённые данным и на комплексной плоскости постройте векторы, изображающие данные числа и комплексно-сопряжённые с ними, запишите матричную форму данных чисел.

а) z = 3 + i; б) z = 3 – i; в) i; г) – 5 i.

№ 3.6. На комплексной плоскости заштрихуйте все точки z, удовлетворяющие условиям

а) |z + i | = 3; б) | z – 1|² + |z + 1|² = 4

в) |z – i | < |z + 2 – 3 i |; г)

д) |z| < |z/2| + 1; е) |z – 1 + i | £ 2.

№ 3.7. Решите уравнения:

а) х² – (4 + 3i)х + 1 + 5i = 0; б) .