Различные формы принципа математической индукции

Помимо уже описанного принципа математической индукции при доказательстве ряда теорем можно также использовать и следующие его вариации.

1) Усиленный принцип математической индукции.

Пусть некоторое утверждение Р(n) сформулировано для всех натуральных чисел, и пусть а) Р(1) – истинно, б) из того, что Р(k) истинно для всех натуральных k меньших, чем некоторое натуральное а, следует, что Р(а) также истинно. Тогда утверждение Р(n) справедливо для всех натуральных чисел.

Доказательство. Предположим, что утверждение Р(n) истинно не для всех натуральных чисел, тогда введём в рассмотрение множество А тех натуральных чисел, для которых утверждение Р(n) ложно. Данное множество не пусто, следовательно, у него имеется наименьший элемент (обозначим его а). Этот элемент не может быть равен 1, так как по условию Р(1) истинно. Таким образом, существуют натуральные числа меньшие, чем а, и все они не принадлежат множеству А, а значит для всех этих элементов утверждение Р(n) истинно. Но из условия (б) теоремы следует, что и Р(а) тоже истинно, что противоречит выбору элемента а. Полученное противоречие возникло из допущения о том, что утверждение верно не для всех натуральных чисел. Поэтому данное предположение неверно, что и доказывает требуемое.

2) Обобщённый принцип математической индукции.

Пусть некоторое утверждение Р(n) сформулировано для всех натуральных чисел n ≥ a (а – некоторое натуральное число), и пусть а) Р(а) – истинно, б) из того, что Р(k) истинно для некоторого k ³ a, следует, что Р(k+1) также истинно. Тогда утверждение Р(n) справедливо для всех натуральных чисел n ³ а.

Доказательство. Предположим, что утверждение Р(n) истинно не для всех натуральных чисел n ³ а, тогда введём в рассмотрение множество А тех натуральных чисел n ³ а, для которых утверждение Р(n) ложно:

А = { n Î N, n ³ a | P(n) – ложь}.

Данное множество не пусто, следовательно, у него имеется наименьший элемент (обозначим его с). Этот элемент с > a, так как Р(а) – истинно. Таким образом, с ≠ 1, так как 1 не может быть больше натурального числа, а значит, число b = c – 1 также является натуральным и при этом не меньше, чем а. b не принадлежит множеству А (так как b < c, а с – наименьший элемент А), следовательно, утверждение Р(b) истинно. Но из условия (б) теоремы следует, что и Р(b + 1) = Р(с) тоже истинно, что противоречит выбору элемента с (с – наименьший элемент множества А, где утверждение ложно). Полученное противоречие доказывает предложение.

3) Обобщённый усиленный принцип полной математической индукции.

Пусть некоторое утверждение Р(n) сформулировано для всех натуральных чисел n ³ a (a Î N), и пусть а) Р(a) – истинно, б) из того, что Р(k) истинно для всех натуральных k, таких что a £ k < c следует, что Р(c) также истинно. Тогда утверждение Р(n) справедливо для всех натуральных чисел n ³ a.

Доказательство: Предположим, что утверждение Р(n) истинно не для всех натуральных чисел n ³ а, тогда введём в рассмотрение множество А тех натуральных чисел n ³ а, для которых утверждение Р(n) ложно:

А = {n Î N, n ³ a | P(n) – ложь}.

Данное множество не пусто, следовательно, у него имеется наименьший элемент (обозначим его с). Этот элемент с > a, так как Р(а) – истинно. Таким образом, существуют натуральные числа k из промежутка a £ k < c, и все они не принадлежат множеству А, а значит для них утверждение Р(n) истинно. Но из условия (б) теоремы следует, что и Р(с) тоже истинно, что противоречит выбору элемента с. Данное противоречие доказывает теорему. Пример. Доказать, что при всех .

Решение. 1) При n = 2 сумма в левой части состоит из двух слагаемых , имеем = .

2) Предположим, что неравенство верно для n = k, , то есть

. Используя это предположение, докажем, что неравенство справедливо при n = k + 1:

.

К правой и левой частям неравенства индукционного предположения прибавим и отнимем (неравенство от этого не изменится). Получим

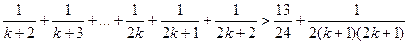
Так как числитель и знаменатель дроби натуральные числа, дробь положительна, а, следовательно, отбрасывание данной дроби усилит данное неравенство:

Следовательно, для n = k +1 неравенство справедливо, и на основании принципа обобщённой математической индукции утверждение доказано.

Задания для самостоятельного решения

№ 1.11. Доказать неравенство для всех натуральных чисел, больших данного n.

а) 3ⁿ > 2ⁿ + n при n > 1 в) 2^n-1 ³ n(n+1) при n > 6

б) 2ⁿ > n² + n +2 при n > 5 г) n² < 2ⁿ при n > 4

д) 2ⁿ < n! при n > 3 ж) n! > при n > 2

е) 2ⁿ > n³ при n > 9 з) 2ⁿ > 2n + 1 при n > 4.

№ 1.12. Доказать неравенство для натуральных чисел n при заданном ограничении

а) 3ⁿ > 5n + 1 при n ³ 3 д) 5ⁿ > 7n – 3 при любом n

б) 4ⁿ > 3ⁿ + 2ⁿ при n ³ 2 е) 3ⁿ > 5n + 1 при n ³ 3

в) > n! при n ³ 3 ж) 4ⁿ > 3ⁿ + n² при n ³ 2

г) 2ⁿ > 2n² - 3n + 1 при n ³ 6 з) 3ⁿ > 5n² при n ³ 4