Гармонические колебания

Определение 4. Простым гармоническим колебанием называется простейшее периодическое явление, в котором расстояние S колеблющейся точки от положения равновесия является функцией времени t: S = A sin(wt + j ₀), где A – амплитуда колебания, w – круговая частота; t – время; j ₀ –начальная фаза (при t = 0); (wt + j ₀) – фаза колебания; Т = 2p/ w – период колебаний.

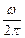– частота колебания, она показывает, сколько периодов укладывается в единицу времени, то есть частоту явления. – круговая частота, она показывает, сколько раз явление повториться за 2p единиц.

Определение 5. График простого гармонического колебания, описываемого уравнением S = A sin(wt + j ₀), называется простой гармоникой.

Пример. Уравнение гармонического колебания имеет вид S = 3sin(2t + 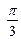). Амплитуда А = 3, круговая частота w = 2, начальная фаза – 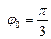, период .

Определение 6. Колебания, получающиеся в результате наложения нескольких простых гармонических колебаний, называется сложными гармоническими колебаниями, а их графики сложными гармониками.

Например, в случае наложения двух простых гармонических колебаний, получаем:

S = A ₁sin(w ₁ t + j ₁) + A ₂sin(w ₂ t + j ₂ ).

Если w ₁ = w ₂ , то результирующее колебание будет снова простым гармоническим колебанием с той же частотой и тем же периодом.

Пусть w ₁≠ w _2. Периоды простых колебаний равны 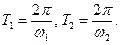Если существует такое число Т, что Т = r ₁ T ₁, T = r ₂ T ₂, то результирующее колебание будет периодическим (r ₁, r ₂ – целые числа). Отсюда вытекает, что Следовательно, частоты w ₁ и w ₂ должны быть соизмеримы. Если частоты несоизмеримы, результирующее колебание не является периодическим. Если частоты соизмеримы, то можно положить w ₁ = r ₁ w ₁, w ₂ = r ₂ w ₂.

Сложное колебание S = A ₁sin(r ₁ wt + j ₁) + A ₂sin(r ₂ wt + j ₂) будет периодическим с периодом Т = 2p/ w.

Пусть . Частоты колебаний, из которых составляется это сложное колебание, образуют гармоническую последовательность, т.е. частоты всех составляющих сложное колебание кратны основной частоте 1/ Т. Колебание с частотой 1/ Т называется первой гармоникой, с частотой 2/Т – второй и т.д.

Пусть w = 1, тогда Т = 2p. К этому всегда можно прийти, изменив масштаб по оси t, т.е. положив wt = t ^/. Суммы простых колебаний(w = 1) 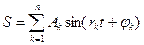при различных значениях параметров А_k, j_k и целых чисел r_k и n приводят к разнообразным периодическим функциям.