Системы линейных однородных уравнений

Определение 4.7. Система линейных уравнений вида:

,

(4.7)

называется однородной системой линейных уравнений, где .

Однородная система всегда имеет одно решение , которое называется тривиальным. Условия с уществования нетривиальных решений определяется следующими теоремами.

Теорема 4.2. Система однородных линейных уравнений имеет нетривиальные решения тогда и только тогда, когда ранг ее матрицы меньше числа неизвестных.

Теорема 4.3. В случае система (4.7) имеет нетривиальное решение только тогда, когда ее определитель равен нулю.

Теорема 4.4. Любая линейная комбинация решений системы (4.7 ) также является решением этой системы.

Определение 4.8. Совокупность решений системы линейных однородных уравнений называется фундаментальной системой решений, если эта совокупность состоит из линейно независимых решений и любое решение системы является линейной комбинацией этих решений.

Теорема 4.5. Если ранг 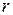матрицы системы (4.7 ) меньше числа неизвестных , то существует фундаментальная система решений, состоящая из решений.

Пример 4.15. Найти общее решение и одну из фундаментальных систем решений для следующей системы однородных уравнений:

.

Решение: 1) Найдем ранг матрицы. Не забываем, что преобразования можно проводить только со строками: {Преобразуем матрицу: умножим первую строку на (-3) и сложим со второй строкой, затем умножим первую строку на (-4) и сложим с третьей строкой, затем умножим первую строку на (-3) и сложим с четвертой строкой}

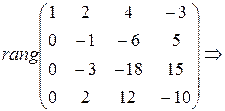{Вторая и четвертая, а также вторая и четвертая строки пропорциональны. Следовательно, третью и четвертую строки можно удалить} , откуда .

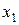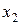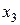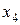2) За базисный минор возьмем определитель . Он имеет наивысший порядок и отличен от нуля. В базисный минор вошли коэффициенты при переменных и , они составят группу зависимых переменных, следовательно, и составят группу свободных переменных.

3) Выразим зависимые переменные через свободные, таким образом, найдем общее решение системы: .

Во втором уравнении умножим все коэффициенты на (-1) и подставим значение 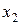из второго уравнения в первое, получим выражения . 4) Найдем фундаментальную систему решений. Она состоит из решений, которые должны быть линейно независимыми. Самый простой способ составить линейно независимые строки в матрице решения это следующий: свободным переменным придают значения из строк определителя 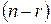-го порядка, отличного от нуля. Затем подставляют эти значения в выражения общего решения и определяют значения зависимых переменных. Простейшим определителем 2-го порядка, отличным от нуля является 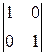. Подставим первый набор значений свободных переменных в решение: 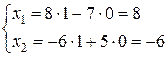, затем второй: . Откуда получаем фундаментальную систему решений: . Ответ: общее решение системы: ; фундаментальная система решений: .