Билет 28

Гипербола – геометрическое место точек, абсолютные величины разности расстояний от которых до двух фиксированных (фокусов) равны.

Введём систему координат так, как показано на рисунке. Здесь, так же, как и у эллипса, , т.е. , . Такая система координат называется канонической. Условие гиперболы записывается так: или . Избавившись от иррациональности (см. вывод уравнение эллипса выше), получим: , где . Уравнение гиперболы в явном виде: .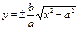

1. Гипербола имеет две оси симметрии (Ox и Oy) и центр симметрии ().

2. Гипербола – гладкая кривая.

3. Уравнение касательной для гиперболы: .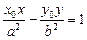

4. Гипербола, задающаяся уравнением , называется сопряжённой для исследуемой гиперболы.

5. - асимптоты гиперболы.

6. и - фокальные радиусы.

7. Эксцентриситет гиперболы , .

8. , .

9. 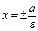- директрисы гиперболы.