 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Polar (radius, ang, minang, maxang)
|
|
выполняет построение графика функции radius(ang), заданной в полярной системе координат, аргумента ang, меняющего значения от minang до maxang.
Приведем несколько примеров.
Пример 1. Построить график функции y = 2е-0,1x cos x (затухающие колебания).
1 способ. В ячейке ввода задаем команду: plot2d(2*exp(0.1*x)*cos(x),[x,0, 20]). После нажатия клавиш Shift+Enter или F5 формируется ячейка ввода в документе
(%i2) plot2d(2*exp(-0.1*x)*cos(x),[x,0,20]);
и открывается окно программы Gnuplot graph с графиком функции:

2 способ. В панели инструментов выбираем кнопку Графики → Plot 2d…, появляется диалоговое окно, в котором предлагается ввести выражение для графика функции, пределы изменения переменной по оси x и y, количество точек графика, выбрать формат для построения графика функции. Например, для построения графика функции y = 2е-0,1x cos x выберем следующие параметры:
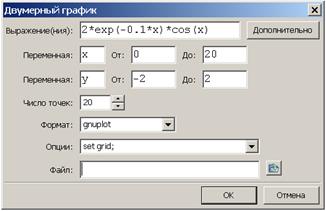
При нажатии на кнопку Ok получим тот же график. Таким образом, можно выбирать наиболее удобный способ построения графиков функций на плоскости.
Пример 2. Построить график параболы 
После нажатия клавиш Shift+Enter или F5 формируется ячейка ввода, которой вводим команду plot2d(3*x**2-2*x-4,[x,-2,3]);
(%i6) plot2d(3*x**2-2*x-4,[x,-2,3]);
и открывается окно программы Gnuplot graph с графиком функции:

Пример 3. Построить график окружности, заданной в параметрической форме

Выполним построение графика параметрически заданной функции следующим образом. Вызываем диалоговое окно для построения графика функции, нажав кнопку Графики → Plot 2d…. В этом окне выбираем Дополнительно → Параметрический график. Открывается диалоговое окно для ввода функции. Заполняем:

Нажимаем на кнопку Ok. Теперь вводим пределы изменения переменных x и y в окне Двумерный график. Нажимаем на кнопку Ok. В результате получаем график:

Пример 4. Построить график неявной функции. В этом случае необходимо воспользоваться пакетом для построения графиков неявно заданных функций implicit_plot. Выполним загрузку пакета:
(%i7) load(implicit_plot)$
Теперь выполняем построение графика эллипса 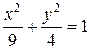 :
:
(%i8) implicit_plot((x^2)/9+(y^2)/4-1,[x,-3,3],[y,-2,2]);

Аналогичным образом построим график гиперболы 
(%i17) implicit_plot((x^2)/2-(y^2)-1,[x,-5,5],[y,-3,3]);

Дата публикования: 2015-07-22; Прочитано: 295 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
