 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Граничний перехід під знаком інтеграла Лебега
|
|
Покажемо, що граничний перехід під знаком інтеграла Лебега можливий при значно слабкіших умовах, ніж у випадку інтеграла Рімана.
Теорема Лебега (про граничний перехід).
Якщо послідовність  сумовних на множині
сумовних на множині  , функцій
, функцій  збігається майже скрізь на
збігається майже скрізь на 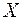 до функції
до функції  , і існує сумовна на
, і існує сумовна на 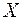 функція
функція  така, що
така, що 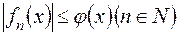 майже скрізь на
майже скрізь на 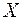 , то функція
, то функція 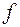 сумовна на
сумовна на 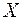 і
і
 (1)
(1)
тобто при вказаних умовах можливий граничний перехід під знаком інтеграла Лебега.
 Перейшовши до границі при
Перейшовши до границі при  в нерівності
в нерівності  дістанемо нерівність
дістанемо нерівність  , справедливу майже скрізь на
, справедливу майже скрізь на 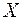 .
.
Звідси випливає 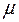 -інтегровність функції
-інтегровність функції 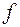 на
на 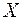 .
.
Задавши довільне число  , розглянемо множини
, розглянемо множини  ,
,
 .
.
Очевидно,  . Оскільки із збіжності майже скрізь випливає збіжність за мірою, то при вказаних в теоремі умовах для довільного
. Оскільки із збіжності майже скрізь випливає збіжність за мірою, то при вказаних в теоремі умовах для довільного  існує номер
існує номер  такий, що
такий, що  при
при  .
.
Позначивши  і враховуючи сказане вище, дістанемо
і враховуючи сказане вище, дістанемо
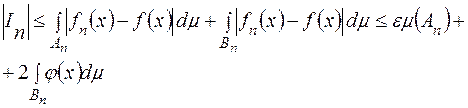 (2)
(2)
Із абсолютної неперервності інтеграла Лебега випливає, що
 . (3)
. (3)
Отже, якщо число  вибрано так, що при заданому
вибрано так, що при заданому  виконується (3), то
виконується (3), то
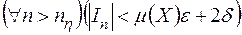 .
.
Оскільки числа  довільні, то із попередньої нерівності випливає, що
довільні, то із попередньої нерівності випливає, що  ,і, отже,
,і, отже,

 .
. 
Наслідок. Якщо виконуються умови попередньої теореми окрім останньої і існує така стала 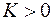 , що
, що  майже скрізь на множині
майже скрізь на множині 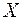 , то функція
, то функція 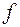
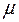 -інтегровна на
-інтегровна на 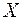 і
і
 .
.
Зауваження. Зазначимо, що твердження із попередньої теореми та наслідку із неї залишаються в силі, якщо умову збіжності майже скрізь на множині 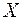 замінити умовою збіжності за мірою на
замінити умовою збіжності за мірою на 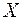 .
.
Приклад. Оскільки послідовність  збігається майже скрізь на
збігається майже скрізь на  до функції
до функції  , і
, і
 , то
, то
 .
.
Теорема Фату. Якщо посліжовність  функцій
функцій  , що невідємні і
, що невідємні і 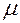 -інтегровні на множині
-інтегровні на множині  , збігається майже скрізь на
, збігається майже скрізь на 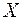 до функції
до функції 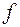 ,
,  , і
, і  , де
, де  , то функція
, то функція 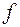
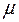 -інтегровна на
-інтегровна на 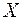 і
і
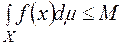
тобто в попередній нерівності можливий граничний перехід під знаком інтеграла.
Теорема Б. Леві. Якщо для послідовності  сумовних на множині
сумовних на множині 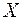 функцій
функцій  виконується
виконується  і
і
 , де
, де  , то майже скрізь на
, то майже скрізь на 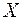 існує скінченна границя
існує скінченна границя
 , функція
, функція 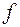 сумовна на
сумовна на 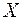 і
і
 .
.
Дата публикования: 2015-07-22; Прочитано: 1244 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
