 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Основні класи множин
|
|
Нехай 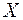 - довільна непорожня множина,
- довільна непорожня множина,  .
.
Означення. Непорожній клас 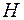 підмножини множини
підмножини множини 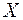 ,
, 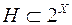 , називається:
, називається:
1) півкільцем, якщо  ,
,  і
і 

 ;
;
2) кільцем, якщо 
 .
.
Зрозуміло, що кожне півкільце 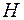 замкнуте відносно операції перетину довільної скінченної кількості множин із нього, тобто
замкнуте відносно операції перетину довільної скінченної кількості множин із нього, тобто 
 .
.
Кожне кільце 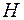 містить порожню множину
містить порожню множину  і воно замкнуте відносно операцій перетину двох множин із нього та утворення симетричної різниці двох множин, що випливає із рівностей
і воно замкнуте відносно операцій перетину двох множин із нього та утворення симетричної різниці двох множин, що випливає із рівностей  ,
,  ,
,  , де
, де  . Зрозуміло, що кільце
. Зрозуміло, що кільце 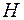 замкнуте відносно об¢єднання та перетину довільної скінченної кількості множин із нього, тобто
замкнуте відносно об¢єднання та перетину довільної скінченної кількості множин із нього, тобто 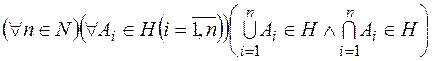 .
.
Очевидно, кожне кільце множин є півкільце множин, але не кожне півкільце є кільце.
Множина  ,
,  , називається одиницею класу множин
, називається одиницею класу множин 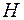 ,
,  , якщо
, якщо  .
.
Кільце з одиницею називається алгеброю множин.
Приклад 1. Сукупність  ,
,  , всіх обмежених підмножин множини
, всіх обмежених підмножин множини 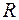 разом із порожньою множиною
разом із порожньою множиною  є кільце без одиниці, тобто
є кільце без одиниці, тобто  не є алгебра множин.
не є алгебра множин.
Приклад 2. Якщо  , то клас
, то клас

піввідкритих паралелепіпедів

метричного простору  разом із порожньою множиною утворює півкільце без одиниці,
разом із порожньою множиною утворює півкільце без одиниці,  . Це півкільце не є кільце, оскільки ні операція об¢єднання множин, ні операція віднімання множин не є замкнутими в
. Це півкільце не є кільце, оскільки ні операція об¢єднання множин, ні операція віднімання множин не є замкнутими в  . Очевидно півкільця
. Очевидно півкільця  ,
,

являють собою сукупності відповідно всіх піввідкритих проміжків  числової прямої
числової прямої 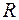 та всіх піввідкритих прямокутників
та всіх піввідкритих прямокутників  координатної площини
координатної площини  разом із порожньою множиною.
разом із порожньою множиною.
Кільце 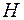 ,
,  , називається
, називається 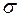 -кільцем (
-кільцем ( -кільцем), якщо воно замкнуте відносно операції об¢єднання (операції перетину) зчисленної сукупності множин із
-кільцем), якщо воно замкнуте відносно операції об¢єднання (операції перетину) зчисленної сукупності множин із 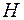 , тобто, якщо для кожної послідовності
, тобто, якщо для кожної послідовності 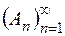 множин
множин 
 виконується
виконується 
 .
.
Можна показати, що кожне 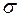 -кільце є
-кільце є  -кільце, але не кожне
-кільце, але не кожне  -кільце є
-кільце є 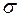 -кільце. Очевидно, кільце із прикладу 1 є
-кільце. Очевидно, кільце із прикладу 1 є  -кільце, що не є
-кільце, що не є 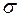 -кільцем.
-кільцем.
Довільне 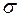 -кільце (
-кільце ( -кільце) множин, що містить одиницю, називається
-кільце) множин, що містить одиницю, називається 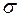 -алгеброю (
-алгеброю ( -алгеброю) множин. Виявляється, що поняття
-алгеброю) множин. Виявляється, що поняття 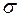 -алгебри та
-алгебри та  -алгебри множин рівносильні (це випливає із законів де Моргана).
-алгебри множин рівносильні (це випливає із законів де Моргана).
Приклад 3. Сукупність 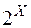 ,
,  , де
, де 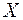 - довільна множина, є
- довільна множина, є 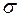 -алгебра множин із одиницею
-алгебра множин із одиницею 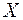 .
.
Дата публикования: 2015-07-22; Прочитано: 1054 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
