Однофакторная классификация

Дисперсионный анализ – метод выделения существующих факторов, в основу которого положено предположение о том, что сущность некоторого фактора характеризуется его вкладом в дисперсию выходной величины.

Дисперсионный анализ является наиболее распространенным методом, базируется на использовании линейных моделей. В качестве исходных данных используются N случайно измеренных значений, которые являются реализациями N случайных переменных и математическое ожидание, которое представляет собой линейную форму от S неизвестных параметров от 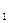а до а .

Д. А. при 1факторной классификации заключается в проверке гипотезы Н, имеющей сл. сод-е:

Н: а₁ = а₂ = … = а_р = 0,

которая означает равное воздействие всех р уровней фактора.

При 1ф. классификации применяются следующие выборочные характеристики:

1. общее среднее:

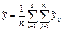
i = 1..p – номер уровня фактора.

j = 1..n_i – номер наблюдения по i-му уровню фактора.

n – общее число наблюдений.

2. среднее по строкам:

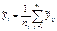
3. сумма квадратов, связанных с рассеянием относительно общего среднего:

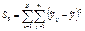
Имеет число степеней свободы φ = n– 1

4.сумма кв., связанная с рассеяниями между уровнями фактора А:

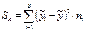
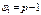
5. сумма квадратов, связанная с рассеяниями внутри отдельных уровней фактора А:

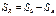
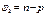
6.

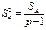
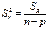
Если гипотеза Н верна, отношение 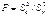будет им. F-распределение.

Находят F_кр - значение функции F-распределения при числах степеней свободы φ₁ и φ₂ и выбранном уровне значимости.

Если F > F_кр, то гипотеза Н отвергается при данном уровне значимости. Это значит, что уровни фактора А влияют на выходную переменную, т.е. она зависит от значений фактора А.