Построение линейных моделей технологических процессов с использованием экспериментальных данных

Пусть требуется на основе экспериментальных данных построить модель процесса. Необходимо сделать предположение о структуре модели. Можно, например, предположить, что взаимосвязь между выходом процесса и независимыми переменными – линейна:

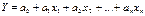
ai –являются неизвестными параметрами процесса, оценки которых требуется найти путём обработки экспериментальных данных.

Пример: примем, что модель линейна относительно коэффициента ai

При этом fi-это известные функции, которые являются компонентами вектора f(x).

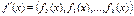
Фактически задача сводится к определению оценки значений вектора коэффициентов и для этого необходимо использовать результаты эксперимента. Оценка выходных величин:

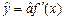, где

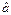-оценка коэффициентов модели.

Если эксперимент проводят в N точках x¹, x², …, x^N с координатами x_i

Результаты наблюдения в точке 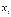представляют с помощью вектора наблюдений:

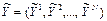
В каждой точке xi может быть поставлено υ экспериментов, результаты которых будут находиться:

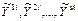
В качестве оценки эксперимента в точке 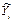можно использовать их среднее значение.

Задача заключается в том, что на основе результатов наблюдений представленных с помощью вектора наблюдений найти наилучшие оценки «â» и «».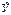

Фактически необходимо сопоставить экспериментальные результаты, отрицающие действительность ( вектор наблюдений) с вектором значений:

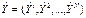- рассчитывается с помощью коэффициента â, отражающего ту или иную модель.

Векторное значение модели можно представить в виде:

Оценка параметров модели â должна удовлетворять условиям:

1.Оценка параметра не должна содержать систематических ошибок;

2. Дисперсия оценки параметров должна быть минимальной.

Эти условия будут выполняться, если:

или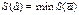

- истинное значение параметров модели.

S- является расширенной, квадратичной формой коэффициентов 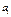, которая имеет единственный минимум при следующих условиях:

- если матрица F имеет ранг (К+1), то сумма квадратов S достигнет минимума при следующих условиях:

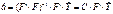
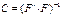
Матрица «С» размером (к+1)*(к+1) называется дисперсионной матрицей. Структура её диагональная:

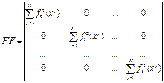
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА