 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Определение величины и направления вектора ускорения Кориолиса точки М
|
|
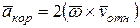 ,
,  ,
,
где  - угол между векторами
- угол между векторами 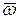 и
и  . По рисунку видно что
. По рисунку видно что  . Тогда
. Тогда  . При
. При  с:
с:


Направление вектора  определим по правилу Жуковского. Спроецируем вектор
определим по правилу Жуковского. Спроецируем вектор 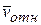 на плоскость, перпендикулярную вектору
на плоскость, перпендикулярную вектору 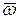 и повернем эту проекцию на 90
и повернем эту проекцию на 90  в сторону вращения. Вектор
в сторону вращения. Вектор  «ляжет» на ось
«ляжет» на ось  и будет направлен на наблюдателя, как показано на рис.3.
и будет направлен на наблюдателя, как показано на рис.3.
5. Определение  . Вектор абсолютной скорости
. Вектор абсолютной скорости  точки М находится по формуле:
точки М находится по формуле:
 (*)
(*)
В данной задаче 
 =
=  , так как
, так как 
 . Но так бывает не всегда, поэтому воспользуемся методом проекций. Равенства (*) перепишем в проекциях на оси неподвижной системы координат
. Но так бывает не всегда, поэтому воспользуемся методом проекций. Равенства (*) перепишем в проекциях на оси неподвижной системы координат 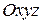 .
.

 ,
, 


 (**)
(**)
Вычислим проекции отдельных векторов скоростей на оси системы координат 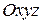 или, что то же самое, на оси системы координат
или, что то же самое, на оси системы координат  и воспользуемся (**). Для момента времени
и воспользуемся (**). Для момента времени  с будет иметь:
с будет иметь:
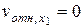 ,
, 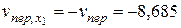 ,
,
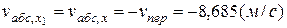 ,
,
 ,
,  ,
, 
 ,
,  ,
,
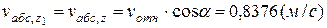
Здесь было учтено, что  ;
;  .
.
Тогда

Косинусы углов  которые вектор абсолютной скорости
которые вектор абсолютной скорости  образует с осями
образует с осями  ,
,  ,
,  , соответственно равны:
, соответственно равны:
 ,
,  ,
,
 ,
,  ,
,
 ,
,  .
.
Вектор  показан на рис. 4 к задаче.
показан на рис. 4 к задаче.
6. Определение  . По () имеем
. По () имеем  . В нашем случае траектория переносного движения точки – окружность радиуса Km, поэтому вектор переносного ускорения
. В нашем случае траектория переносного движения точки – окружность радиуса Km, поэтому вектор переносного ускорения  . Тогда
. Тогда
 (***)
(***)
В проекциях на оси неподвижной системы координат (***) примет вид:
 ,
,  ,
,
 . (****)
. (****)
Вычислим проекции векторов 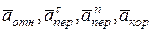 , входящих в (***), на оси неподвижной системы координат
, входящих в (***), на оси неподвижной системы координат 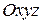 .
.
 ,
,  ,
,  .
.
 ,
,  ,
,  ,
,
 ,
,  .
.
Подставляя полученные выражения проекций в (****), для момента  получим:
получим:
 =
= 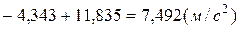 ,
,  =
=  ,
,
 =
=  .
.

 .
.
Косинусы углов  , которые вектор
, которые вектор  образуют с осями
образуют с осями  соответственно равны
соответственно равны
 ,
, 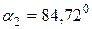 ,
,
 ,
,  ,
,
 ,
,  .
.
Вектор  показан на рис.4 к задаче.
показан на рис.4 к задаче.
Задача 5.2. Ползун  движется вдоль прямолинейной кулисы
движется вдоль прямолинейной кулисы  от точки
от точки  к точке
к точке  с постоянной скоростью
с постоянной скоростью  , а сама кулиса вращается вокруг оси
, а сама кулиса вращается вокруг оси  , перпендикулярной плоскости рисунка, с угловой скоростью
, перпендикулярной плоскости рисунка, с угловой скоростью 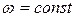 . Принимая ползун за точку, определить абсолютную скорость и абсолютное ускорение ползуна
. Принимая ползун за точку, определить абсолютную скорость и абсолютное ускорение ползуна  в момент времени, когда ползун переместиться на расстояние
в момент времени, когда ползун переместиться на расстояние 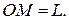
Решение: Движение ползуна вдоль кулисы для ползуна является относительным движением, а вращательное движение кулисы – переносным движением. Поэтому  и модули этих векторов равны
и модули этих векторов равны  . Переносная скорость
. Переносная скорость  . Вектор
. Вектор  перпендикулярен
перпендикулярен  , а модуль абсолютной скорости ползуна будет равен
, а модуль абсолютной скорости ползуна будет равен  Так как
Так как  , то
, то  .
.  (так как
(так как 
 )
)  Модуль кориолисова ускорение находится по формуле
Модуль кориолисова ускорение находится по формуле 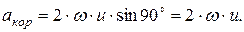 Модуль абсолютного ускорения при
Модуль абсолютного ускорения при  будет равен
будет равен  . Здесь
. Здесь  (
(
Ответ: 

Задача 5.3. Точка  движется с постоянной скоростью
движется с постоянной скоростью  по кольцу радиуса
по кольцу радиуса  , которое вращается с постоянной угловой скоростью
, которое вращается с постоянной угловой скоростью  относительно оси
относительно оси  Определить модуль абсолютного ускорения точки
Определить модуль абсолютного ускорения точки  в указанном на рисунке положении.
в указанном на рисунке положении.

Решение: Движение точки по кольцу – это её относительное движение, вращение кольца вместе с кольцом – переносное движение. Тогда (т.к. 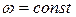 ):
):  ,
, 




 Учитывая, что
Учитывая, что  получим
получим  т.к.
т.к. 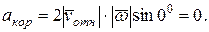
Дата публикования: 2015-07-22; Прочитано: 1710 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
