Теорема о геометрическом сложении векторов скоростей при сложном движении точки

5.8. Теорема. При сложном движении точки вектор скорости точки в абсолютном движении геометрически складывается из вектора скорости в относительном движении точки и вектора скорости в переносном движении точки:

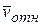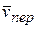= + (5.1)

Доказательство: Пусть точка 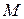движется по некоторому телу, а само тело совершает какое-либо движение в неподвижной системе отсчета с системой координат 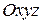(рис.5.1). С телом жестко связана подвижная система координат 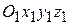, которая на рисунке не показана. Определим вектор скорости точки 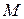в абсолютном движении, то есть при движении точки в неподвижной системе координат 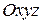, в фиксированный момент времени . На рис. 5.1 изображены два положения точки, соответствующие моментам времени и . Время, в течении которого произошло перемещение точки в пространстве равно . 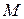В момент времени движущаяся точка находилась в точке пространства . В момент времени точка 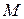переместилась в точку пространства . Следовательно, вектор - вектор абсолютного перемещения точки .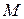

Абсолютное перемещение точки 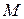есть следствие относительного перемещения точки в подвижной системе координат 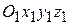по траектории относительного движения и перемещения этой траектории, как жесткого целого, в неподвижной системе координат 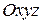. При этом - вектор переносного перемещения точки 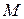. Траектории относительного движения изображены на рисунке в соответствующие моменты времени в виде кривых и . Фактически, кривые и - это одна и та же пространственная кривая в два момента времени и по-разному ориентированная по отношению к неподвижной системе координат 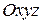(кривые и совпали бы при наложении). Из рисунка видно, что

(5.2)

Поделив равенство (5.2) на и переходя к пределу, будем иметь:

= (5.3)

По формуле (1.13) и определению 5.5 предел, стоящий в левой части равенства (5.3) равен вектору абсолютной скорости , первый предел, стоящий в правой части по формуле (1.13) и определению 5.6 равен вектору переносной скорости 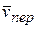. Принимая во внимание, что при кривая стремиться к кривой , можно заключить, что

Тогда (5.3) принимает вид:

= +

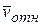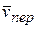
Что и требовалось доказать. Графическое представление равенства (5.1) приведено на рис. 5.2.

При непосредственном использовании равенства (5.1) нужно помнить, что для конкретного момента времени графически изображается диагональю параллелограмма, построенного на векторах 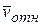, 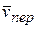. Из равенства (5.1) может быть определен один любой из входящих в него векторов.

Теорему (5.1) можно записать и в виде метода проекций. Спроецируем равенство (5.1) на оси произвольной системы координат. Тогда будем иметь:

= + ; = + ;

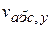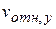= + . (5.4)

= = . (5.5)

Косинусы углов (направляющие косинусы) вычисляются по формулам:

; ;

(5.6)