Ознака Даламбера

Нехай ряд U1+U2+….+Un+….- З ДОДАТНІМИ ЧЛЕНАМИ. Припустимо, що існує границя , тоді якщо .

Наприклад, ;

Un =; Un+1=; 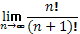= = 0<1, збіжний.

59.Ознаказбіжності ряду. Для того щоб ряд 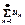збігався, необхідно, щобзагальний член ряду прямував до нуля, тобтощобвиконуваласьумова

Доведення. Нехай ряд збігається, тобтоіснуєграницячастиннихсум ряду

З рівності u_n = S_n – S_{n– 1}випливає, щоіснуєграниця

що і доводить правильністьтеореми. Умова не є достатньою для збіжності ряду, щоможнабачити на прикладі так званого гармонійного ряду

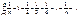
60)Інтегральна ознака збіжності ряду

Якщо функція f(х) неперервна,додатна і монотонно спадає при х,більше дор 1, то ряд

І невласний інтеграл dx збігається або розбігається

Ознака Коші (радикальна)). Якщо для ряду з додатними членами існує границя , тоді: при 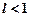ряд збігається;при ряд розбігається;при питання про збіжність ряду ознака не вирішує. (Ознака Коші ( інтегральна )). Якщо функція 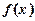неперервна, додатна і монотонно спадає при то ряд і невластивий інтеграл збігаються або розбігаються разом.

61 Ознака Лейбніца

Теорема 13 (Лейбніца). Якщо члени знакопочергового ряду спадають за абсолютною величиною і границя абсо-
лютної величини загального члена ряду дорівнює нулю, то ряд збігається. Коротко цю теорему можна записати так:

Наслідок 1. Знак суми збіжного знакопочергового ряду такий само, як і знак першого члена ряду. Наслідок 2. Якщо знакопочерговий ряд збігається, то його сума за абсолютною величиною не перевищує першого члена ряду, тобто Наслідок 3. Якщо при обчисленні суми збіжного знакопочергового ряду обмежитись тільки першими n членами, а всі інші відкинути, то похибка за абсолютною величиною не перевищить першого із відкинутих членів, тобто 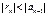. Наслідок 4. Якщо для ряду не виконується умова теореми Лейбніца , то ряд розбігається (не виконується необхідна умова збіжності).

62Абсолютна і умовна збіжність ряду.

Означення. Ряд називається знакозмінним, якщо він містить нескінченне число як додатних, так і від’ємних членів.

Теорема 12 (Коші). Якщо збігається ряд із абсолютних величин членів знакозмінного ряду, то збігається і знакозмінний ряд, тобто

Означення. Знакозмінний ряд називається абсолютно збіжним, якщо збігається ряд із абсолютних величин членів знакозмінного ряду.Означення. Знакозмінний ряд називається умовно збіжним, якщо цей ряд збігається, а ряд із абсолютних величин його членів розбігається.Зауваження. Якщо знакозмінний ряд збігається абсолютно, то його збіжність зумовлена достатнім спаданням за абсолютною величиною його членів.Зауваження. Якщо знакозмінний ряд збігається умовно, то його збіжність зумовлена не тільки спаданням за абсолютною величиною його членів, але і взаємною компенсацією додатних і від’ємних членів ряду.

63. Перша теорема Абеля: Нехай ряд є збіжним в точці x ₀. Тоді цей ряд є абсолютно збіжним в кругу | x | < | x ₀ |рівномірно по x на будь-якій компактній підмножині цього круга.Навпаки, якщо степеневий ряд є розбіжним при x = x ₀, він є розбіжним при всіх x, таких що | x | > | x ₀ |. З першої теореми Абеля також випливає, що існує такий радіус круга R (можливо, нульовий або нескінченний), що при | x | < R ряд є абсолютно збіжним (і збіжність є рівномірною по x на компактних підмножинахкруга| x | < R), а при | x | > R ряд є розбіжним. Це значення R називається радіусом збіжності ряду, а круг | x | < R — кругом збіжності. Якщо степеневий ряд:

1) збігається при х = х ₀, то він абсолютно збігається для будь-якого х, що задовольняє нерівність ;

2) якщо ряд

розбігається при х = х ₁, то він розбігається при всіх х, що задовольняють нерівність

64.Радіус збіжності

Означення. Інтервалом збіжності степеневого ряду називається такий інтервал, у всіх внутрішніх точках якого ряд збігається абсолютно, а для всіх точок ряд є розбіжним; при цьому число R > 0 називається радіусом збіжності степеневого ряду.

Виведемо формулу для знаходження радіуса збіжності ряду . Для цього побудуємо ряд із абсолютних величин членів ряду: (1):

(9.14)

Нехай існує границя . Тоді, застосовуючи ознаку Даламбера до ряду (2), дістаємо:

При ряд (2) збігається, а отже, ряд (1) збігається абсолютно; при ряд (2) розбігається. Розбіжність ряду, установлена за ознакою Даламбера, означає, що для цього ряду не виконується необхідна умова збіжності: , а тому не виконується необхідна умова збіжності і для ряду (1) 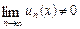, і ряд (1) при буде також розбіжним. Отже, нерівність визначає інтервал збіжності ряду (2): . Радіус збіжності визначається за формулою

.

65.. Наближенеінтегрування за доп.рядів

Степеневий ряд

буде рівномірно збіжним на будь-якому відрізку із його інтервалу збіжності , а тому на такому відрізку його можна почленно інтегрувати та диференціювати, при цьому мають місце рівності:

66.. Ряд Фурє

Функція , що задовольняє умови Діріхле на відрізку на інтервалі може бути визначена тригонометричним рядом Фур’є: (9.26)

де коефіцієнти Фур’є та обчислюються за такими формулами:

Зауваження. Якщо функція — парна, то в (9.26) , а якщо — не парна, то .

Теорема 18 (ознака Діріхле). Якщо — періодична функція з періодом 2π задовольняє умови Діріхле на відрізку , то її ряд Фур’є збіжний, а його сума в точці х ₀ дорівнює:

1. 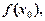якщо — неперервна в точці х ₀;

2. якщо — точка розриву для

67.Означення. Диференціальним рівнянням називається рівняння, яке містить похідну шуканої функції. Найбільший порядок похідних називається порядком диференціального рівняння.

У загальному випадку диференціальне рівняння n -го порядку має вигляд

Як правило, ДР має нескінченну множину розв’язків. Так, диференціальне рівняння у ¢ = 2 у має розв’язок у = Се ^{2 х} , де С — довільний сталий параметр.

Якщо шукана функція у = у (х) залежить від одного аргументу, то ДР для у (х) називається звичайним.

Якщо шукана функція залежить від кількох аргументів, то маємо ДР зчастинними похідними. У цьому розділі викладаються лише звичайні ДР.

Означення. ДР виду

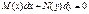(13)

називається ДР з відокремленими змінними. Загальний розв’язок ДР знаходимо з рівняння

Розв’язок задачі Коші з початковими умовами х = х ₀, у = у ₀ має вигляд

Знаходження розв’язку ДР з відокремленими змінними зводиться до квадратур, тобто до пошуку інтегралів від відомих функцій. Означення. ДР виду

N ₁(y) M ₁(x) dx + M ₂(x) N ₂(y) dy = 0 (14)

називається ДР з відокремлюваними змінними, тобто таким, що зводиться до ДР з відокремленими змінними.

Поділимо рівняння (14) на функцію N ₁(y) M ₂(x) і дістанемо ДР з відокремленими змінними

яке має інтеграл

ДР (14) також має розв’язки у = у_k, x = x_j, де у = у_k є коренем рівняння N ₁(y) = 0, а x = x_j є коренем рівняння M ₂(x) = 0 (особливі розв’язки).

Аналогічно, ДР виду

y ¢ = f (x) g (y)

є ДР з відокремлюваними змінними.

Рівняння (15) можна записати у вигляді

Рівняння (15) має також розв’язок у = у_k, де g (у_k) = 0.

69. Однорідні ДР 1 порядку

ДР називається однорідним, якщо його можна подати у вигляді

(16)

ДР (16) за допомогою заміни змінної у

зводиться до ДР з відокремлюваними змінними

і пошук розв’язку зводиться до квадратур

70.. Лінійні ДР 1-го порядку

Рівняння, що є лінійним відносно невідомої функції та її похідної, називається лінійним диференціальним рівнянням. Його загальний вигляд такий:

.

Якщо , тобто рівняння має вигляд

,

то воно зветься однорідним. Однорідне рівняння є рівнянням зі змінними, що розділяються і розв’язується таким чином:

Нарешті .

Розв’язок неоднорідного рівняння будемо шукати методом варіації довільних сталих (методом невизначених множників Лагранжа). Він складається в тому, що розв’язок неоднорідного рівняння шукається в такому ж вигляді, як і розв’язок однорідного, але вважається невідомою функцією від , тобто і . Для знаходження підставимо у рівняння

.

Звідси

Проінтегрувавши, одержимо

.

І загальний розв’язок неоднорідного рівняння має вигляд

Якщо використовувати початкові умови , то розв’язок можна записати у формі Коші:

.

71. Рівняння Бернуллі

Рівляння виду

де п не дорівнює нулю або одиниці, називається рівнянням Бернуллі. Якщо п = 0, то рівняння збігатиметься з лінійним. Якщо п = 1, то після об'єднання Р (х) з Q(x) дістанемо лінійне од­норідне рівняння

метод розв'язування якого відомий. Тому цікаво розглянути рівнян­ня, в якому п 0 або п 1. Розв'яжемо рівняння. Поділивши його на уⁿ, знайдемо

Введемо позначення у^-n+1 = z, тоді

73. деякі типи диф. Р-нянь що припуск. Зниж порядків

1.

2.

3.

Зведення рівняння вищого порядку до системи рівнянь

Вводячи змінні , звичайне диференціальне рівняння можна записати у вигляді системи звичайних диференціальних рівнянь першого порядку

74.Структура заг.розв.лінйного неоднорідного ДР.

Шукаємо загальний розв’язок неоднорідного ДР у вигляді .

Оскільки виконується тотожність , то для відшукання z маємо однорідне ДР

Отже, справджується така теорема:

Теорема 1. Загальний розв’язок неоднорідного лінійного ДР дорівнює сумі частинного розв’язку неоднорідного ДР і загального розв’язку однорідного ДР.

. Метод варіації довільних сталих.

Лагранж запропонував загальний метод розв’язування неоднорідних лінійних ДР. Спочатку розв’язується однорідне ДР.
У загальний розв’язок входять довільні сталі. Потім шукається загальний розв’язок неоднорідного ДР і при цьому довільні сталі стають новими шуканими функціями.Шукатимемо розв’язок неоднорідного ДР (8.29).

Спочатку розв’яжемо однорідне ДР . Загальний розв’язок має вигляд . Шукаємо розв’язок неоднорід­ного ДР у вигляді 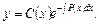Підставляючи в ДР (8.28), дістаємо рівняння

.Приходимо до простого ДР

і загального розв’язку неоднорідного ДР виду (8.30):

Метод Лагранжа часто називають методом варіації довільної сталої.

76) Рівняння виду y’’+py’+qy=0

p,q –постійні коефіцієнти; y₁, y₂

ȳ = C₁y₁+C₂y₂

Нехай:

y=e^kx; k – поки що невідоме стале число

y’=ke^kx

y’’=k²e^kx

k²e^kx+pke^kx+qe^kx=0

k²+pk+q=0

1) k₁≠k₂ – дійсні прості числа

y₁=e^k₁^x

y₂=e^k₂^x

y₂/y₁=e^k₂^x/e^k₁^x ≠ const –лінійно-незалежне рівняння

2) Коплексні спряжені корені

k₁=ɣ+δi; k₂=ɣ-δi

y₁=e^ɣxcosδx; y₂=e^ɣxsinδx

y₂/y₁ = e^ɣxcosδx/e^ɣxsinδx=tgδx≠const

3) k₁=k₂=k

y₁=e^kx

y₂=xe^kx

y₂/y₁ = x ≠ const

77 Рівня виду З(х)е

Теорема 3. Якщо права частина лінійного диференціального рівняння із сталими коефіцієнтами має вид , де - многочлен n -ої степені і не є коренем характеристичного рівняння, то існує частинний розв'язок вигляду , де - деякий многочлен n -ої степені:

. Якщо ж є коренем характеристичного рівняння кратності k ( або ), то існує частинний розв'язок вигляду .

Зокрема, при права частина - многочлен n -ої степені, і якщо не є коренем характеристичного рівняння, то частинний розв'язок - також деякий многочлен тієї ж степені. Якщо ж - корінь кратності k, то частинний розв'язок має вигляд .

78 Рівня виду Р(х)

Кос

Теорема 4. Якщо ж права частина лінійного диференціального рівняння із сталими коефіцієнтами може бути подана у вигляді

,
де і - многочлени (n - найбільша з їх степенів) і не є коренем характеристичного рівняння, то існує частинний розв'язок виду

,
де

і -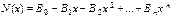

многочлени степені n. Якщо ж є коренем характеристичного рівняння кратності k, то існує частинний розв'язок виду

.

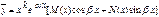Приклад. Вирішити рівняння .

Розв'язок. Вирішимо відповідне однорідне рівняння . Складемо характеристичне рівняння ; його корені , . Загальний розв'язок відповідного однорідного рівняння є .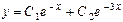

Тому що права частина даного неоднорідного рівняння має вид 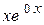(тобто вид ), причому 0 не є коренем характеристичного рівняння , то частинний розв'язок будемо шукати у виді

.

Підставимо цей вираз в задане рівняння

, .

, .

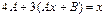Прирівнюючи коефіцієнти при однакових степенях х, получимо

Відкіля , . Отже, . Загальний розв'язок буде

.

79. Розв.лінійного неоднорідного рівняння н-го порядку.

ДР виду

називається лінійним ДР n -го порядку. Якщо то ДР називається однорідним, якщо то ДР називається неоднорідним.

80. Системи ДР

ДР

завжди можна звести до системи рівнянь виду

(8,54) (8.54)

Загальний розв’язок системи рівнянь (8,54) має вигляд

де — довільні сталі. Система рівнянь

визначає s -й частинний розв’язок системи рівнянь (8.54). Ці розв’язки будуть лінійно незалежні, якщо

81.Метод Ейлера.

Домножуємо рівняння 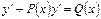на інтегрувальний множник Дістаємо ДР

Нехай ДР набирає вигляду:

.

Остаточно приходимо до розв’язку виду

:

82.наближене розвязування диференціальних рівнянь за допомогою степеневих рядів.

Записати три перших, відмінних від нуля, члени розкладу в степеневий ряд за степенями розв’язку диференціального рівняння що задовольняє початкову умову

Р о з в ’ я з о к. Розв’язок даного диференціального рівняння запишемо у вигляді ряду за степенями

Із рівняння знаходимо Диференціюючи рівняння по одержимо

і

і

Тоді