 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теор про границю
|
|
Нехай послідовності х(н)і у(н) мають відповідні границі а і в, тоді
Лім(х +у)= лімх + ліму=а+в
Лім(ху)+дімх*ліму
Лімхпод1л на лімх аде вне дорівн нулю
18. Перша визначна границя. .Друга визначна границя
Перша особлива границя 
Границі — наслідки першої особливості границі:
1.  2.
2. 
3.  4.
4. 
Зауваження. За допомогою першої особливої границі можна досліджувати невизначеності  для виразів з тригонометричними функціями.
для виразів з тригонометричними функціями.
Для того щоб скористатися першою особливою границею, потрібно виконати таку заміну змінної х, щоб нова змінна прямувала до нуля, наприклад 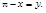
.Друга визначна границя. Друга особлива границя 
Границі — наслідки другої особливої границі:
1.  . 2.
. 2.  .
.
3.  .
.
4.  .
.
Зауваження: За допомогою другої особливої границі та її на-
слідків можна досліджувати невизначеності
 .
.
Сума, різниця, добуток і частка від ділення двох неперервних функцій також неперервна (для частки – за винятком тих значень аргументів, що перетворюють на нуль знаменник), тобто, якщо  і
і  неперервні в точці
неперервні в точці  , то в цій точці будуть неперервними і функції
, то в цій точці будуть неперервними і функції

19.Неперервність функції. Дії над неперервнимифу-ми
Функція  називається неперервною в точці
називається неперервною в точці  якщо
якщо 
Виходячи з означення границь функції, поняття неперервності функції в точці можна зобразити так:

Звідси випливає, що для неперервності функції в точці мають виконуватися такі умови:
а) точка х = х 0 належить області визначення функції  тобто
тобто  існує;
існує;
б) деякий окіл точки х = х 0 входить до області визначення функції, наприклад 
в) границя  при
при 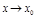 дорівнює значенню функції в точці х = х 0, тобто дорівнює
дорівнює значенню функції в точці х = х 0, тобто дорівнює  .
.
Позначимо через 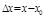 приріст аргументу, а через
приріст аргументу, а через  — приріст функції
— приріст функції
Функція називається неперервною в деякій точці, якщо ця функція визначена в якому-небудь околі даної точки, і якщо границя приросту функції дорівнює нулю, коли приріст аргументу прямує до нуля.
Сума скінченного числа функцій, неперервних у деякій точці, є функцією, неперервною в цій точці.
Різниця скінченного числа функцій, неперервних у деякій точці, є функцією, неперервною в цій точці.
Добуток скінченного числа функцій, неперервних в деякій точці, є функцією, неперервною в цій точці.
Відношення двох функцій, неперервних у деякій точці, є функцією, неперервною в цій точці, якщо дільник не дорівнює нулю.
20. Теореми про функції,неперервні на замкненій множині.
Т Якщо ф-ія неперервна в точці, то вона обмежена деяким околом цієї точки.
Т. Якщо ф-ії f(x;y) та g(x;y) неперервні в точці (x0;y0), то в цій точці будуть неперервними f(x;y)±g(x;y), f(x;y)×g(x;y), f(x;y)/g(x;y) при g(x0;y0)¹0
Т(1-ша т Вейєрштрасса). Якщо ф-ія неперервна на замкнутій множині, то вона обмежена на цій площині.
Т(1-га т В). Якщо ф-ія неперервна на замкнутій обмеженій множині, то серед її значень є як найменші, так і найбільші.
Т(Больцано-Коші) Нехай ф-ія неперервна на зв’язній множині D і приймає у двох точках А і В цієї множини значення різних знаків. тоді у множині D знайдеться така точка, що в ній ф-ія обертається в нуль.
Т(2-га т Б-К) Нехай ф-ія f(x;y) неперервна на зв'язаній множині D і у двох будь-яких точках А та В цієї множини вона приймає будь-яке значення m, яке лежить між f(A) і (B), тобто існує така точка cÎD, що f(c)= m.
21. Точки розриву та їх класифікація.
. Функція  називається розривною в точці
називається розривною в точці  якщо порушується хоча б одна з умов рівності
якщо порушується хоча б одна з умов рівності

Розриви 1-го роду бувають усувні й неусувні; розриви 2-го роду — завжди неусувні.
Точка  називається точкою розриву 2-го роду для функції
називається точкою розриву 2-го роду для функції  , якщо в цій точці не існує хоча б одна з односторонніх границь (зліва чи справа).
, якщо в цій точці не існує хоча б одна з односторонніх границь (зліва чи справа).
Точка  називається точкою розриву 1-го роду (розрив неусувний) для функції
називається точкою розриву 1-го роду (розрив неусувний) для функції  , якщо односторонні границі (зліва і справа) функції у цій точці існують, але не рівні між собою, тобто
, якщо односторонні границі (зліва і справа) функції у цій точці існують, але не рівні між собою, тобто 
22. Похідна,її фізичний,геометричний,економічний зміст.
Похідною функції  за аргументом х називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.
за аргументом х називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.
Дотичною до кривої L у точці М називається граничне положення МN січної ММ 1 при прямуванні точки М 1 по кривій L до точки М
Нехай крива, задана рівнянням  , має дотичну в точці М (х, у). Позначимо (рис. 4.2) кутовий коефіцієнт дотичної МN:
, має дотичну в точці М (х, у). Позначимо (рис. 4.2) кутовий коефіцієнт дотичної МN:  . Надамо в точці х приросту
. Надамо в точці х приросту  , тоді ордината у набуде приросту
, тоді ордината у набуде приросту  .
.
З  випливає, що
випливає, що  . Коли
. Коли  , то
, то 
 і січна прямує до положення дотичної МN.
і січна прямує до положення дотичної МN.
Таким чином,  Оскільки
Оскільки  , то
, то  тобто похідна
тобто похідна  чисельно дорівнює кутовому коефіцієнту дотичної, проведеної до графіка функції у точці з абсцисою х. У цьому полягає геометричний зміст похідної.
чисельно дорівнює кутовому коефіцієнту дотичної, проведеної до графіка функції у точці з абсцисою х. У цьому полягає геометричний зміст похідної.
Механічний зміст похідної
Припустимо, що точка М рухається прямолінійно нерівномірно по деякій прямій лінії, яку візьмемо за вісь Ох (
Рух точки відбувається за законом х = f (t), де х — шлях; t — час. Знайдемо швидкість точки М у да-ний момент часу t (миттєва швидкість).
Нехай точка М у момент t перебувала на відстані х від початкової точки М 0, а в момент часу  точка опинилася
точка опинилася
на відстані  від початкової точки й зайняла положення М 1. Отже, час t набув приросту
від початкової точки й зайняла положення М 1. Отже, час t набув приросту  , а шлях х — приросту
, а шлях х — приросту  . Середня швидкість руху точки М за час
. Середня швидкість руху точки М за час  описується формулою
описується формулою  .
.
Якщо точка М рухається рівномірно, то V cр є величина стала, і її беруть за швидкість точки. Для нерівномірного руху точки очевидно, що для достатньо близьких значень  до нуля середня швидкість точки М буде близька до її швидкості у момент часу t. Тому за точне значення швидкості точки М у момент часу t беруть величину
до нуля середня швидкість точки М буде близька до її швидкості у момент часу t. Тому за точне значення швидкості точки М у момент часу t беруть величину
 ,
,
яка є швидкістю зміни функції х = f (t) у точці. У цьому полягає механічний зміст похідної. Розглянемо задачу про продуктивність праці. Нехай функція  відображає кількість виробленої продукції u за час t і необхідно знайти продуктивність праці в момент t 0.
відображає кількість виробленої продукції u за час t і необхідно знайти продуктивність праці в момент t 0.
За період часу від t 0 до  кількість виробленої продукції зміниться від значення
кількість виробленої продукції зміниться від значення  до значення
до значення  ; тоді середня продуктивність праці за цей період часу
; тоді середня продуктивність праці за цей період часу  . Очевидно, що продуктивність праці в момент t 0 можна визначити як граничне значення середньої продуктивності за період часу від t 0 до
. Очевидно, що продуктивність праці в момент t 0 можна визначити як граничне значення середньої продуктивності за період часу від t 0 до 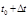 при
при  , тобто
, тобто
 .
.
Таким чином, продуктивність праці є похідна від обсягу виробленої продукції по часу.
23 Логарифмічна похідна
логарифмічна похідна фунції f виз формулою.

де f ′ похідна функції f.
Коли f функція f (x) від дійсної змінної x, і приймає дійсні, суворо додатні значення, логарифмічна похідна дорівнює похідній від ln(f); або, похідній натурального логарифма f.
що логарифм добутку дорівнює сумі логарифмів множників

Таким чином для додатньо-дійсних функцій, логарифмічна похідна добутку це сума логарифмічних похідних множників. Але ми також можемо використати тотожність Лейбніца для знаходження похідної добутку

Таким чином, вірно те, що для будь-яких функцій логарифмічна похідна добутку це сума логарифмічних похідної множників (де вони визначені).
Аналогічно, (в дійсності це наслідок), логарифмічна похідна оберненої функції є логарифмічна похідна первісної функції помножена на − 1:

як і у випадку із логарифмом оберненого додатнього числа.
Більш загально, логарифмічна похідна ділення це різниця логарифмічних похідних діленого і дільника:

як і логарифм дробу дорівнює різниці діленого і дільника.
Узагальнюючі в іншому напрямку, логарифмічна похідна степеня (з константним дійсним показником) є добутком показника і логарифмічної похідної основи:

як і логарифм степеня є добутком показника і логарифма основи.
24. Правило Лопіталя.
Нехай Ф(х) та Д(х) неперервні та мають похідні в усіх х не = а з околу точки х = а, а в точці а рівні нулю або нескінченості.Тоді
Тео (правило Лопіталя). Границя відношення двох нескінченно малих або нескінченно великих функцій дорівнює границі відношення їхніх похідних (скінченній або нескінченній), якщо остання існує.
Зауваження. Якщо  і
і  при
при  прямують одно-часно до 0 або до ¥ і задовольняють ті умови, які були накладені теоремою на функції
прямують одно-часно до 0 або до ¥ і задовольняють ті умови, які були накладені теоремою на функції  і
і  , то до відношення
, то до відношення  /
/  знову застосовуємо правило Лопіталя і виводимо формулу
знову застосовуємо правило Лопіталя і виводимо формулу

25. Похідна неявно заданої функції та функції,заданої параметрично
Похідна складної функції. Нехай у = f (u), де  , тобто
, тобто  . Функція f (u) називається зовнішньою, а функція
. Функція f (u) називається зовнішньою, а функція  — внутрішньою, або проміжним аргументом.
— внутрішньою, або проміжним аргументом.
Теорема 6. Якщо у = f (u) та  — диференційовні функції від своїх аргументів, то похідна складної функції існує і дорівнює
— диференційовні функції від своїх аргументів, то похідна складної функції існує і дорівнює  .
.
Таким чином, похідна складної функції дорівнює добутку похідної зовнішньої функції за проміжним аргументом на похідну проміжного аргументу за незалежною змінною.
Похідна оберненої функції. Нехай задані дві взаємно обернені диференційовні функції
у = f (х) та  .
.
Теорема 7. Похідна  оберненої функції
оберненої функції  по змінній у дорівнює оберненій величині похідної
по змінній у дорівнює оберненій величині похідної  від прямої функції
від прямої функції  .
.
Похідна неявної функції. Нехай рівняння F (x; y) = 0 визначає у як неявну функцію від х. Надалі будем вважати, що ця функція — диференційовна. Продиференціювавши за х обидві частини рівняння F (x; y) = 0, дістанемо рівняння першого степеня відносно  . З цього рівняння легко знайти
. З цього рівняння легко знайти  , тобто похідну неявної функції.Похідна параметрично заданої функції. Нехай функцію
, тобто похідну неявної функції.Похідна параметрично заданої функції. Нехай функцію  від
від  задано параметричними рівняннями:
задано параметричними рівняннями:  .Припустимо, що функції
.Припустимо, що функції  мають похідні і що функція
мають похідні і що функція  має обернену функцію
має обернену функцію  , яка також є диференційовною. Тоді визначену параметричними рівняннями функціо-
, яка також є диференційовною. Тоді визначену параметричними рівняннями функціо-
нальну залежність 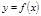 можна розглядати як складну функцію
можна розглядати як складну функцію  ,
,  (
( — проміжний аргумент).
— проміжний аргумент).
На підставі теорем 6 та 7 маємо:
 ,
,  .
.
Звідки 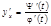 або
або  .
.
26. Диференціал та його геометричний зміст.
Добуток F’(x)*Dx назив. диференціалом ф-ції у=f(x), зображують символом dy, тобто dy=f’(x)* Dx.
Знайдемо диференціал ф-ції у=х; для цього випадку y’=x’=1, отже dy=dx=Dx. Таким чином диференціал не залеж змінної збігається з її приростом Dx. Þ dy=f’(x)dx
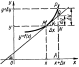
PN y, QN MN tg x f x f x dx dy.
Отже, диференціал функції f x при заданих
значеннях x і x дорівнює приросту ординати дотичної до
кривої y f x в точці x.
Таким чином, заміна приросту функції на її диференціал геометрично означає заміну ординати АР кривої ординатою дотичної AQ. Зрозуміло, що така заміна доцільна лише для достатньо малих значень  х.
х.
27.Частинна похідна.
Нехай ф-ція z=f(x;y) має частинні похідні в усіх т. множ. D. Візьмемо т. (х;у) є D. В цій точці існують частинні похідні ¶z/¶x і ¶z/¶y, які залеж від х та у, тобто є ф-ціями 2 змін. Значить можна поставити питання про знаходж її частинних похідних. Якщо вони існують, то назив похідними ІІ порядку  .
. 
Знайдена формула дає можливість знаходити похідну  від параметрично заданої функції, не знаходячи явної залежності
від параметрично заданої функції, не знаходячи явної залежності 
28. Градієнт, похідна в заданому напрямку.
Напрям найбільшої швидкості зміни ф-ції z=f(x;y) співпадає з напрямом вектора – градієнтом.
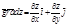

За формулою довж вектора знаходять величину цієї найбільшої швидкості:

Градієнт, як завжди вважають, — векторна величина, яка визначає в кожній точці простору не лише швидкість зміни, а й напрямок найшвидшої зміни функції, що залежить від координат. Але при замінах координат, градієнт перетворюється інакше, ніж вектор, і тому його не можна розглядати як справжній вектор.
Для скалярного поля 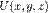 градієнт визначається формулою
градієнт визначається формулою

Це означення узагальнюється на простори будь-якої розмірності
 .
.
29. Формула Тейлора (випадок функції однієї та двох змінних).
ейлора формула

Rn(х)залишок
Ф(х) =Рн(х), х=а
Ф(1)(х)=Рн(х), х=а
Ф(11)(х)=Р(1)н(х), х=а
Ф(н)(х)=Рн(н)(х), х=а
30Досліджн ф-їза доп похід 1 і 2 пор

31Вертикальні та похилі асимптоти
це пряма, до якої крива при видаленні в нескінченність наближається як завгодно близько.
Якщо крива, задана рівнянням y = f(x), віддаляється в нескінченність при наближення x до скінченної точки a, то пряма x = a називається вертикальною асимптотою цієї кривої.
Вертикальну асимптоту функції задають координатою точки х=х(нульове) через яку проходить відповідна вертикальна пряма. Похилу асимптоту функції задають коефіцієнтами а(нульове) і а(1) і лінійної функції у- а(1)помнож на х + а(нульове)
Вертикальні асимптоти.
Пряма х = А є вертикальною асимптотою, якщо границя цієї функції дорівнює нескінченності при аргументі, що прямує до А.
Пряма у = В є горизонтальною асимптотою, якщо границя цієї функції дорівнює числу В при аргументі, що прямує до нескінченності.
Пряма y = kx + b є похилою асимптотою, якщо границя відношення функції до її аргументу дорівнює числу k при аргументі, що прямує до нескінченності і якщо границя різниці функції і kx дорівнює числу b при аргументі, що прямує до нескінченності.
Якщо
 , або
, або  ,
,
або  , то пряма х = а є вертикальною асимптотою для графіка функції
, то пряма х = а є вертикальною асимптотою для графіка функції  .
.
Похилі асимптоти. Нехай крива  має похилу асимптоту
має похилу асимптоту  , тоді
, тоді
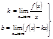 .
.
Якщо хоча б одна з границь не існує, то крива похилих асимптот у відповідній напівплощині не має.
32. Екстремум функції двох змінних.
Нехай ф-ія z=f(x;y) визначена в деякому околі точки (x0;y0) і неперервна в цій точці. Якщо для всіх точок (x;y) цього околу виконується нерівність  , тоді ця точка (x0;y0) називається точкою максимуму (мінімуму) ф-ії z=f(x;y).
, тоді ця точка (x0;y0) називається точкою максимуму (мінімуму) ф-ії z=f(x;y).
Точки максимуму і мінімуму наз. точками екстремуму.
Теорема (необхідна умова екстремуму): Якщо ф-ія z=f(x;y) має екстремум в точці (x0;y0), тоді в цій точці частинні похідні  і
і  або дорівнюють нулю, або хоча б одна з них не існує.
або дорівнюють нулю, або хоча б одна з них не існує.
Теорема (достатня умова екстремуму): Нехай ф-ія має екстремум у точці (x0;y0), неперервні частинні похідні першого і другого порядку, причому  та
та  а також
а також 

 . Якщо:
. Якщо:
1) AC-B2>0 і A<0 тоді (x0;y0) точка максимуму
2) AC-B2>0 і A>0 тоді точка мінімуму
3) AC-B2<0 екстремуму немає
4) AC-B2=0
33. Задача про умовний екстремум – постановка і способи розв’язування.
Нехай на відкритій множині D Ì R2 задано ф-ії u=f(x;y), v= j (x;y) і Е – множина точок, що задовольняють рівняння: 
Означення: Рівняння  називають рівнянням зв’язку, точку (x0;y0)ÎЕ називають точкою умовного строгого максимуму ф-ії u=f(x;y) при обмеженнях рівняння.
називають рівнянням зв’язку, точку (x0;y0)ÎЕ називають точкою умовного строгого максимуму ф-ії u=f(x;y) при обмеженнях рівняння.
Точки умовного максимуму та мінімуму називають точками умовного екстремуму. Умовний екстремум інколи називають відносним екстремумом
Класична задача на умовний екстремум — задача умовної оптимізації, допустима множина X якої має вигляд:

тоді, класичну задачу на умовний екстремум можна записати так:

34.Комплексні числа та дії з ними в алгебраїчній формі.
Комплексним числом називається число виду  , де a, b — дійсні числа, і2 = – 1. Число а називається дійсною частиною, bi — уявною частиною, і — уявною одиницею. Множина комплексних чисел позначається С
, де a, b — дійсні числа, і2 = – 1. Число а називається дійсною частиною, bi — уявною частиною, і — уявною одиницею. Множина комплексних чисел позначається С
. Комплексні числа виду a + bi і a – bi називаються спряженими. Комплексні числа виду a + bi і – a – bi називаються протилежними. Спряжене до комплексного числа z позначається  .
.
. Два комплексних числа a + bi і a1 + b1i вважаються рівними в тому і тільки в тому випадку, якщо a = a1 і b = b1.Зауваження. Щодо комплексних чисел не прийнято жодної угоди, яке з них вважати більшим.
Додавання: (a + bi) + (a 1 + b 1 і) = (a + a 1) + (b + b 1) i.
Віднімання: (a + bi) – (a 1 + b 1 i) = (a – a 1) + (b – b 1) i.
Множення: (a + bi)(a 1 + b 1 i) = aa 1 + a 1 bi + ab 1 i + bb 1 i 2=(aa 1 – bb 1) + (a 1 b + ab 1) i.
Ділення:
 Піднесення до степеня: спочатку знайдемо результати від піднесення до степеня уявної одиниці, знаючи, що за умовою і 2 треба вважати таким, що дорівнює – 1.
Піднесення до степеня: спочатку знайдемо результати від піднесення до степеня уявної одиниці, знаючи, що за умовою і 2 треба вважати таким, що дорівнює – 1.
35. Комплексні числа та дії з ними в тригонометричній форм
Додавати і віднімати комплексні числа простіше і зручніше, коли компоненти подані в алгебраїчній формі. Зовсім інша річ з останніми чотирма алгебраїчними діями. Множення. Нехай треба перемножити числа:  ,
,  .
.
Дістанемо: 
Звідси випливає:Модуль добутку двох комплексних чисел дорівнює добуткові модулів співмножників, а аргумент — сумі аргументів співмножників.
36.Невизначений інтеграл та його геометрична інтерпретація.
Функція F (x) + С, що являє собою загальний вигляд всієї множини первісних для функції f (x) на проміжку І, називається невизначеним інтегралом від функції f (x) на проміжку І і позначається
 ,
,  ,
,
де  — знак невизначеного інтеграла;
— знак невизначеного інтеграла;
f (x) — підінтегральна функція;
f (x) dx — підінтегральний вираз;

dx — диференціал змінної інтегрування.
Геометричний зміст невизначеного інтеграла полягає в тому, що функція  є рівняння однопараметричної сім’ї кривих, які утворюються одна з одної паралельним перенесенням уздовж осі ординат
є рівняння однопараметричної сім’ї кривих, які утворюються одна з одної паралельним перенесенням уздовж осі ординат
37.Властивості невизначеного інтеграла
а) Властивості, що випливають із означення  ,
, 
І.Похідна від невизначеного інтеграла дорівнює підінтегральній функції  .
.
ІІ. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу.
ІІІ.  .
.
б) Властивості, що відображають основні правила інтегрування.
IV. Сталий множник, що не дорівнює нулю, можна виносити з-під знака інтеграла, тобто

V. Невизначений інтеграл від суми функцій дорівнює сумі невизначених інтегралів від цих функцій, якщо вони існують, тобто
 ,
, 
38.Метод підстановки (заміна змінної інтегрування)інтегрування частинами
Мета методу підстановки — перетворити даний інтеграл до такого вигляду, який простіше інтегрувати.
Теорема 4. Якщо f (x) — неперервна, а 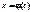 має непе-
має непе-
рервну похідну, то:

Наслідок.

Зауваження. Специфіка інтегрування невизначеного інтеграла не залежить від того, є змінна інтегрування незалежною змінною чи сама є функцією (на підставі інваріантності форми запису першого диференціалу), тому, наприклад:
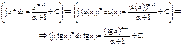
У такому розумінні слід розглядати і всю таблицю інтегралів.
Інтегрування частинами
Теорема 3. Якщо функції u (x) та v (x) мають неперервні похідні, то:

На практиці функції u (x) та v (x) рекомендується вибирати за таким правилом:
— при інтегруванні частинами підінтегральний вираз  розбивають на два множники типу u × dv, тобто
розбивають на два множники типу u × dv, тобто  ; при цьому функція u (x) вибирається такою, щоб при диференціюванні вона спрощувалась, а за dv беруть залишок підінтегрального виразу, який містить dx, інтеграл від якого відомий, або може бути просто знайдений
; при цьому функція u (x) вибирається такою, щоб при диференціюванні вона спрощувалась, а за dv беруть залишок підінтегрального виразу, який містить dx, інтеграл від якого відомий, або може бути просто знайдений
39-40.Інтегрування раціональних дробів.Найпростіші дроби
Відношення двох многочленів  називається раціональним дробом.
називається раціональним дробом.
Раціональний дріб  називається правильним, якщо степінь многочлена в чисельнику менший від степеня многочлена в знаменнику, тобто n < m; якщо n ³ m, то дріб називається неправильним.
називається правильним, якщо степінь многочлена в чисельнику менший від степеня многочлена в знаменнику, тобто n < m; якщо n ³ m, то дріб називається неправильним.
Теорема 5. Будь-який неправильний раціональний дріб можна подати у вигляді суми многочлена (цілої частини) та правильного раціонального дробу.
За домовленістю найпростішими раціональними дробами називаються такі дроби чотирьох типів:
І.  ; ІІ.
; ІІ.  ; ІІІ.
; ІІІ.  ; IV.
; IV.  ,
,
де  , інтеграли від яких мають вигляд
, інтеграли від яких мають вигляд
І.  ;
;
ІІ. 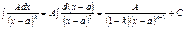 ;
;
ІІІ.
 — розглянуто в (7.1.9);
— розглянуто в (7.1.9);
IV.
 — інтегрується за допомогою рекурентних формул.
— інтегрується за допомогою рекурентних формул.
Теорема 6. Будь-який правильний раціональний нескоротний дріб  можна подати у вигляді скінченної кількості найпростіших дробів, використовуючи такі правила:
можна подати у вигляді скінченної кількості найпростіших дробів, використовуючи такі правила:
1). Якщо  , то
, то
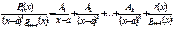 ;
;
2). Якщо  то
то 
 ,
,
де Аі, Ві, і = 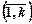 — деякі коефіцієнти,
— деякі коефіцієнти,  та
та  — правильні раціональні дроби
— правильні раціональні дроби
42.Інтегрування диференціального бінома Підстановки Ейлера
Інтеграл від диференціального бінома має вигляд
 ,
,
де  — раціональні числа.
— раціональні числа.
За теоремою Чебишова цей інтеграл може бути зведено до інтегрування раціональних функцій лише у таких випадках:
1.  , підстановка
, підстановка  , де
, де  — найменше спільне кратне знаменників дробів
— найменше спільне кратне знаменників дробів  та
та  .
.
2.  — ціле, підстановка
— ціле, підстановка 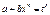 , де
, де  — знаменник дробу
— знаменник дробу  .
.
3.  — ціле, підстановка
— ціле, підстановка  , де
, де  — знаменник дробу
— знаменник дробу 
Підстановки ейлера
- підстановки, за допомогою яких інтеграли вигляду
 де R (х, у) - раціональна функція від х і у, зводять до інтегралів від раціональних функцій. Запропонував Л. Ейлер 1768. Розрізняють такі Е. п.:
де R (х, у) - раціональна функція від х і у, зводять до інтегралів від раціональних функцій. Запропонував Л. Ейлер 1768. Розрізняють такі Е. п.:
 де? - один з 2-х коренів тричлена ах2 + bх + с, якщо цей тричлен має дійсні корені.
де? - один з 2-х коренів тричлена ах2 + bх + с, якщо цей тричлен має дійсні корені.
|
43.Інтег-я тригонометричних ф-й. Універсальна тригонометрична підстановка.
Універсальна тригонометрична підстановка наз вираз тригонометричних функцій через тангенс половиного аргумента. тоді підстановка sin х = cos х =  dx=
dx=
Інтегрування тригонометричних функцій
Інтеграли вигляду
А) 


Б) 
Для обчислення інтегралів даного вигляду застосовують тригонометричні формули.
Cos(a) cos(b) = ½(cos(a-b)+cos(a+b)
Sin(a) sin(b) = ½(cos(a-b)-cos(a+b)
Sin(a) cos(b)-1/2(sin(a-b)+sin(a+b)
44.Поняття визначеного інтеграла. Геометричний зміст визначеного інтеграла
Нехай  — деяка функція, що задана на проміжку [ a; b ]. Розіб’ємо [ a; b ] на n частин точками
— деяка функція, що задана на проміжку [ a; b ]. Розіб’ємо [ a; b ] на n частин точками  так що
так що

Обчислимо  де
де 


Складемо інтегральну суму  .
.
Позначимо 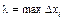 .
.
. Якщо існує скінченна границя інтегральних сум Sn при  і не залежить ні від способу розбиття [ a; b ] на частини
і не залежить ні від способу розбиття [ a; b ] на частини  , ні від вибору точок
, ні від вибору точок  , то ця границя називається визначеним інтегралом від функції
, то ця границя називається визначеним інтегралом від функції  на проміжку [ a; b ] і позначається:
на проміжку [ a; b ] і позначається:
 ,
,
де  — знак визначеного інтеграла;
— знак визначеного інтеграла;
а, b — нижня та верхня межі інтегрування;
f (x) — підінтегральна функція;
f (x) dx — підінтегральний вираз;
dx — диференціал змінної інтегрування.
Геометричний зміст визначеного інтеграла
Якщо  , то
, то  дорівнює площі відповідної криволінійної трапеції
дорівнює площі відповідної криволінійної трапеції

45.Формула Ньютона-Лейніца.
Якщо функція  — неперервна для
— неперервна для  то визначений інтеграл від функції
то визначений інтеграл від функції  на проміжку
на проміжку  дорівнює приросту первісної функції
дорівнює приросту первісної функції  на цьому проміжку, тобто
на цьому проміжку, тобто
 де
де 
Позначимо дію подвійної підстановки так: 
тоді зв’язок між визначеним та невизначеним інтегралами можна подати такою рівністю:
 Наслідок. Для обчислення визначеного інтеграла достатньо знайти одну із первісних підінтегральних функцій і виконати над нею подвійну підстановку.
Наслідок. Для обчислення визначеного інтеграла достатньо знайти одну із первісних підінтегральних функцій і виконати над нею подвійну підстановку.
46.Заміна змінних у визначеному інтегралі.Інтегрування частинами у визначеному інтегралі
Якщо: 1)  — неперервна для
— неперервна для 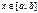 ; 2)
; 2) 
 3)
3)  та
та  — неперервні для
— неперервні для  4) при
4) при  то
то

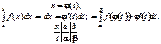 Зауваження. При заміні змінної інтегрування у визначеному інтегралі змінюються межі інтегрування, і тому нема потреби повертатись до початкової змінної.
Зауваження. При заміні змінної інтегрування у визначеному інтегралі змінюються межі інтегрування, і тому нема потреби повертатись до початкової змінної.
Інтегрування частинами у визначеному інтеграліТеорема 11. Якщо функції  та
та  мають неперервні похідні для
мають неперервні похідні для  , то
, то 
47.Невласні інтеграли 1 і 2 роду.
. Границя  при
при  називається невласним інтегралом від функції f(x) на нескінченному проміжку
називається невласним інтегралом від функції f(x) на нескінченному проміжку  і позначається так:
і позначається так:  .
.
Якщо ця границя існує та скінченна, то невласний інтеграл називається збіжним, а якщо не існує (зокрема нескінченна), то — розбіжним.Якщо f (x) — інтегровна для скінченних a та b, тобто  формули для обчислення невласних інтегралів на нескінченному проміжку мають вигляд:
формули для обчислення невласних інтегралів на нескінченному проміжку мають вигляд:



де 
48.Обчислення площі в декартових координ
Якщо на відрізку  задана неперервна функція
задана неперервна функція  то згідно з геометричною інтерпретацією визначеного інтеграла площа криволінійної трапеції, обмеженої кривою
то згідно з геометричною інтерпретацією визначеного інтеграла площа криволінійної трапеції, обмеженої кривою 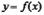 прямими
прямими  ,
,  та віссю
та віссю  (рис. 1, а), обчислюється згідно з формулою:
(рис. 1, а), обчислюється згідно з формулою:


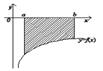
трапеції (а – якщо  , б – якщо
, б – якщо  )
)
Якщо на відрізку  функція
функція  (рис. 1, б), то криволінійна трапеція буде розміщена у нижній півплощині і відповідний визначений інтеграл буде від’ємним. Оскільки площа фігури є величиною невід’ємною, то її можна розрахувати за формулою:
(рис. 1, б), то криволінійна трапеція буде розміщена у нижній півплощині і відповідний визначений інтеграл буде від’ємним. Оскільки площа фігури є величиною невід’ємною, то її можна розрахувати за формулою:
 ,
,  (1.2)
(1.2)
Якщо на відрізку  функція
функція  декілька разів змінює знак (рис. 2), то інтеграл на відрізку
декілька разів змінює знак (рис. 2), то інтеграл на відрізку  треба поділити на суму інтегралів по часткових відрізках – відрізках знакосталості функції. Інтеграл буде додатним на тих відрізках, на яких
треба поділити на суму інтегралів по часткових відрізках – відрізках знакосталості функції. Інтеграл буде додатним на тих відрізках, на яких  , та від'ємним там, де
, та від'ємним там, де  . Інтеграл на відрізку
. Інтеграл на відрізку  дає різницю площ фігур, що лежать вище та нижче від осі
дає різницю площ фігур, що лежать вище та нижче від осі


Рис. 2. Геометрична інтерпретація інтеграла від знакозмінної функції 
Щоб знайти суму площ без урахування розташування щодо осі  , треба знайти суму абсолютних значень інтегралів на відрізках знакосталості функції або обчислити інтеграл від абсолютного значення функції, тобто (рис. 3)
, треба знайти суму абсолютних значень інтегралів на відрізках знакосталості функції або обчислити інтеграл від абсолютного значення функції, тобто (рис. 3)


49. Обчислення площі в полярних координ
Інтегральне числення


Область R, яка утворена полярною кривою r (φ) та променями φ = a та φ = b.
Нехай R — область, яку утворюють полярна крива r (φ) і промені φ = a та φ = b, де 0 < b − a < 2π. Тоді площа цієї області знаходиться визначеним інтегралом:



Область R наближно утворена з n секторів (тут, n = 5).
Такий результат можна отримати наступним чином. Спочатку розіб’ємо інтервал [ a, b ] на довільне число підінтервалів n. Таким чином довжина такого підінтервалу Δφ дорівнює b − a (повна довжина інтервалу) поділена на n (число підінтервалів). Нехай для кожного підінтервалу i = 1, 2, …, n φ i — середня точка. Побудуємо сектори з центром у полюсі, радіусами r (φ i), центральними кутами Δφ і довжиною дуг  . Тому площа кожного такого сектора буде
. Тому площа кожного такого сектора буде  . Звідси, повна площа всіх секторів:
. Звідси, повна площа всіх секторів:

Якщо число підінтервалів n збільшувати, то похибка такого наближеного виразу буде зменшуватися. Поклавши n → ∞, вищеотримана сума стане інтегральною. Границя цієї суми при Δφ → 0 визначає вищеописаний інтеграл:

Дата публикования: 2015-07-22; Прочитано: 600 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
