 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Довжина дуги в полярних координат
|
|
Нехай рівняння кривої L в полярних координатах 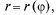
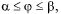 при чомуфункція
при чомуфункція 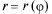 неперервнодиференціюючи на [а,b]. Використовуючи формули переходувідполярних координат до декартовихіберучи за параметр кут
неперервнодиференціюючи на [а,b]. Використовуючи формули переходувідполярних координат до декартовихіберучи за параметр кут 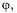 маємопараметричнірівняння кривої
маємопараметричнірівняння кривої 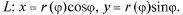 Тоді
Тоді
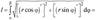
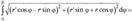
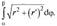
Наприклад: Вычислить длину дуги логарифмической спирали
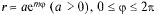 (рис. 18.10).
(рис. 18.10).
Рис. 18.10

52. Застосування інтегралів в економіці
Визначення загального обсягу випущеної продукції Нехай деяка фірма випускає один вид продукції, використовуючи один ресурс. Виробнича функція фірми має вигляд q=q(x), де x - затрати ресурсу, а q - обсяг випуску. Затрати ресурсу x є функцією від часу t, наприклад, x=x(t).Тоді загальний обсяг продукції Q за час від T0 до T1 обчислюється за допомогою визначеного інтегралу.При, x(t)=100e0,2t, T0=0 та T1=5 (років) загальний обсяг випущеної за п’ять років продукції2. Визначення коефіцієнта Джинні Нехай y=y(x) - частка (доля) приватного капіталу деякої країни, яка перебуває у власності групи людей, що становлять частку (долю) x населення цієї країни.Наприклад, у тому випадку, коли 30% населення володіє 10% капіталу, 60% населеня 35% капіталу, і 85% 60% капіталу, маємо таке:y(0,3)=0,1;y(0,6)=0,35;y(0,85)=0,6.
Очевидно, що завжди y(0)=0 та y(1)=1.
53.Подвійний інтеграл та його обчислення
. Якщо 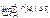 існує та не залежить ні від способу розбиття області D на частини, ні від вибору точок Mi, то ця границя називається подвійним інтегралом від функції
існує та не залежить ні від способу розбиття області D на частини, ні від вибору точок Mi, то ця границя називається подвійним інтегралом від функції 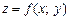 по області D і позначається так:
по області D і позначається так:
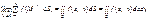
Заміна змінних інтегрування в подвійному інтегралі
Нехай у подвійному інтегралі (7.36) треба зробити перехід від змінних 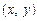 до змінних
до змінних 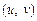 , тобто перейти від декартової системи координат
, тобто перейти від декартової системи координат  до довільної системи координат
до довільної системи координат 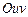 за формулами
за формулами 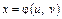 ,
, 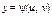 , які відомі.
, які відомі.
Для цього необхідно обчислити елементарну площу 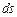 в новій системі координат
в новій системі координат 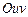 .
.
Диференціал радіуса-вектора в системі 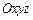 має вигляд:
має вигляд:
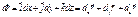 .
.
Отже, елементарну площу 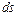 у декартовій системі координат можна знайти як модуль векторного добутку векторів:
у декартовій системі координат можна знайти як модуль векторного добутку векторів:
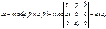 .
.
У довільній системі координат 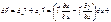

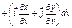 , а елементарна площа буде такою:
, а елементарна площа буде такою:
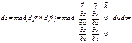
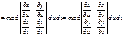
Дата публикования: 2015-07-22; Прочитано: 735 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
