Означення суми ряду

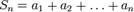Нехай - числовий ряд. Число називається n-ої часткової сумою ряду 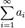.Сума (числового) ряду - це межа часткових сум Sn, якщо він існує і кінечний. Таким чином, якщо існує число 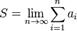, то в цьому випадку пишуть 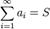. Такий ряд називається збіжним. Якщо межа часткових сум не існує або нескінченний, то говорять, що ряд розходиться.

55.Властивості числових рядів

1 На збіжність ряду не впливає додавання чи відкидання скінченного числа доданків,

2 Уявимо, що ряд U₁+U₂+…+U_n+… (1)-числовий ряд збігається і сума його = S,тоді утворимо такий ряд CU₁+CU₂+…+CU_n+… (2), ряд 2 теж збігається і сума його =cS,

3 Нехай ми маємо такий ряд V₁+V₂+…+V_n+…(3) збігається і з нього можна утворити такий (U₁+-V₁)+(U₂+-V₂)+… (U_n+-V_n)+… (4), то він буде рядом збіжним і його сума S+-S₁

56. Необхідна ознака зб ряду:

Яко ряд U₁+U₂+…+U_n+… (1) збігається, то його n-ий член прямує до 0(U_nпрямуэ до0, т прямуэ до безкынечносты), якщо ряд збігається, то його ряд прямує до 0(оберненетвердження не вірне).

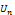=, гармонійний ряд- є рядом розбіжним не дивлячись на те, що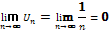

Необх ознаку зручно викор як достатню ознаку розбіжн числов рядів

57Ознака порівняння. Нехай задано два знакододатні числові ряди:

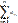, (a_n>=0),(1)

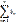, (b_n>=0), (2)

та для всіх n виконується нерівність a_n<=b_n

Тоді, якщо ряд (2) збіжний, то

збіжний і ряд (1). Якщо ряд (1) розбіжний, то розбіжний і ряд (2).

Напри домі 1поділ на н*2 в степені н…ряд буде збіжн бо знамен більше 1.

Ознака порівняння в граничній формі. Нехай задано два числові ряди (1),

(2). Якщо існує скінченна, відмінна від нуля границя 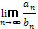=A,то обидва

ряди збігаються, або розбігаються одночасно

.