Резонанс напряжений

Характерные признаки резонанса напряжений перечислены ранее. Напомним их. Резонанс напряжений возникает в последовательном контуре R, L, C (рис. 2.1.) при условии равенства индуктивной и емкостной составляющей полного сопротивления. При этом напряжения на реактивных элементах U _L и U _C полностью компенсируют друг друга, а результирующее напряжение равно напряжению на активном сопротивлении U _R и совпадает по фазе с входным током (рис. 1.14.).

Рис. 2.1.

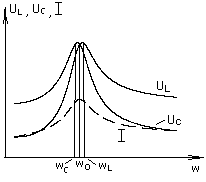
Зависимость параметров последовательного контура с известными параметрами R, L и C от частоты питающего напряжения иллюстрируется резонансными кривыми, рис. 2.2. и рис. 2.3., построенными при изменении частоты постоянного по модулю входного напряжения от 0 до .

Функции U_L и U_C имеют следующие аналитические выражения:

; (2.2)

; (2.3)

Рис 2.2.

Отметим характерные особенности приведенных зависимостей. Функции имеют явно выраженные максимумы соответственно при частотах и . Максимум напряжения на конденсаторе наступает при частоте, меньшей чем резонансная, , так как на интервале [0, ] сопротивление X_C постепенно убывает при одновременном возрастании тока, в то время как при ток и сопротивление убывают одновременно.

Рис.2.3.

Аналогичные рассуждения можно провести и для доказательства справедливости . Ниже эти логические рассуждения будут доказаны математически.

Функция модуля тока от частоты имеет вид:

. (2.4)

I(w) имеет максимум I₀ в момент резонанса . При этом , и 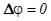(ток и напряжение на входе совпадают по фазе).

При возрастании частоты от 0 до разность (X_L-X_C)< 0 и убывает. Соответственно ток в цепи возрастает от нуля до максимума. Аналогично рассуждая, можно объяснить характер кривых I и на участке .

Резонансные кривые на рис. 2.3. подтверждают, что в момент резонанса разность фаз входного тока и напряжения равна нулю и при его прохождении характер цепи меняется с емкостного на индуктивный.

Резонансные кривые могут быть построены не только для конкретного контура, но и для обобщенного контура, если использовать такие связующие его R, L и С параметры, как уже названная резонансная частота , а также характеристическое (волновое) сопротивление и добротность контура.

Характеристическое сопротивление r контура определяется соотношением его индуктивной и емкостной составляющих:

r . (2.5)

Такое определение взято не случайно. Ранее отмечалось, что в момент резонанса напряжение на реактивном элементе превышает напряжение на входе всей цепи. Это возможно при условии R<w₀L или Rw₀C<1.

Так как , то оба эти условия приводятся к виду

или R < r.

Заметим, что при резонансе и , а выражение (2.5) для волнового сопротивления дает отношение величины напряжения на индуктивном элементе к величине тока в цепи в момент резонанса:

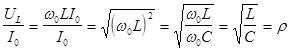. (2.6)

Величина, равная отношению волнового сопротивления контура к последовательно включенному активному сопротивлению, называется добротностью:

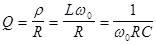. (2.7)

Добротность - важный параметр резонансного контура. Экспериментально добротность контура можно определить в момент резонанса как отношение напряжения на реактивном элементе к входному напряжению цепи. Далее будет показано, что Q можно определить также по резонансной кривой. Чем выше Q, тем меньшее количество энергии рассеивает контур на активном сопротивлении в момент резонанса, тем лучше его энергетические показатели. Однако получение реального контура с Q>10 вызывает значительные технические трудности.

Рассмотрим зависимость формы кривой U_L от параметра добротности контура.

Преобразуем выражение 2.2, введя в него параметр добротности контура. Для этого выразим из (2.7)

,

и введем понятие относительной частоты:

. (2.8)

Уравнение 2.2 после подстановки примет вид:

Выполнив преобразования, окончательно получим

, (2.9)

где - параметр, характеризующий расстройку контура и подробно рассматриваемый в конце этого параграфа.

Аналогично рассуждая, получим . (2.10)

Значения относительных частот, при которых U_L и U_C имеют максимум, можно найти, продифференцировав (2.9) и (2.10) относительно h. В результате получим:

. (2.11) . (2.12)

Анализируя (2.11) и (2.12), перейдем к следующим выводам:

1) При , кривые U_C(w) и U_L(w) максимумов не имеют.

2) При заданной добротности контура всегда h_С<1 и h_L>1.

Последнее следует и из частотных характеристик сопротивлений контура (рис. 2.3.). На интервале частот [0,w₀] X_C>X_L и, следовательно, U_C >U_L, а при w >w₀, X_C < X_L, и соответственно U_C <U_L.

3) Частоты максимумов U_L и U_C (соответственно w_L и w_C) равны только при условии Q>>0. Однако при Q>5 с погрешностью 1%,справедливо U_L(w_L)=U_C(w_C)=UQ.Последнее утверждение можно проверить на практическом примере расчета реального контура в файле rezon_u.mcd приложений.

Волновое сопротивление r и добротность контура Q определяют внешний вид его резонансных кривых и позволяют построить обобщенные резонансные кривые для сравнения характеристик контуров с разным сочетанием значений R, L и C.

Обобщенные резонансные кривые для контуров с различной Q

(рис. 2.4.) - это зависимости .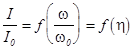

Отметим, что ,где . (2.13)

Преобразуем выражение для Z с учетом (2.7):

Рис. 2.4.

Подставив в (2.13), получим:

. (2.14)

Формы кривых затухания при различных Q приведены на рис. 2.4.

Анализируя вид кривых и выражения (2.14), можно сделать следующее замечание.

Чем выше добротность контура, тем острее резонансная кривая и тем меньшая площадь заключена под кривой и, следовательно, меньшее количество энергии рассеивается контуром во всем диапазоне рассматриваемых частот. Контур с высокой добротностью имеет лучшие энергетические характеристики и избирательную способность. Последняя определяется шириной полосы пропускания контура,

рис. 2.5.

На графике резонансной кривой полоса пропускания контура определяется как разность относительных частот h₁-h₂ (рис. 2.5.), при которой ток в контуре в меньше I₀ резонансного тока. В этот момент полное сопротивление контура Z в раз больше минимального, равного R. Константа выбрана не случайно. При этом значении резонансная частота равна среднему геометрическому граничных частот полосы пропускания .

Докажем это, воспользовавшись выражением (2.14).

При 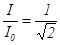, получим .

Решив и преобразовав уравнение, получим .

Отсюда , (2.15)

и . (2.16)

Складывая эти выражения, получим .

Последнее равенство справедливо только при условии h₁h₂=1 или .

Анализируя (2.14), можно утверждать, что при 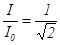, ширина полосы пропускания равна величине .

Действительно, вычитая (2.16) из (2.15), получим ,

поскольку , имеем .

Последнее равенство служит обоснованием метода определения величины Q по резонансной кривой.

Расстройкой контура называют параметр .

При w<w₀, расстройка имеет отрицательные значения, а при w>w₀ - положительные. Если контур подключен к источнику с частотой, такой, что w₁ <w < w₂, то для него .

Приведенные выше рассуждения рекомендуется проанализировать при помощи файла rezon_u.mcd приложения.